 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема (необходимый признак существования экстремума)
|
|
Если 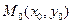 - точка экстремума (максимума, или минимума) функции
- точка экстремума (максимума, или минимума) функции 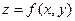 , в которой она имеет частные производные, то
, в которой она имеет частные производные, то 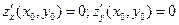 .
.
При этом надо заметить, что функция 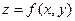 может иметь экстремум также и в тех точках, где хотя бы одна из частных производных не существует. Точки, в которых первые частные производные
может иметь экстремум также и в тех точках, где хотя бы одна из частных производных не существует. Точки, в которых первые частные производные 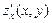 и
и 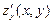 обращаются в нуль или не существуют, называются критическими. Точки, в которых частные производные существуют и равны нулю, называются стационарными.
обращаются в нуль или не существуют, называются критическими. Точки, в которых частные производные существуют и равны нулю, называются стационарными.
Пусть 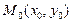 - стационарная точка функции
- стационарная точка функции 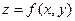 . Значения вторых производных функции в стационарной точке обозначим так:
. Значения вторых производных функции в стационарной точке обозначим так: 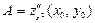 ,
, 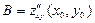 ,
, 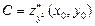 .
.
Из этих чисел составим определитель 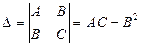 .
.
Дата публикования: 2014-11-04; Прочитано: 270 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
