 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Аудиторная контрольная работа
|
|
Задачи 1 – 20. Вычислить интегралы:
1. а)  ; 2. а)
; 2. а) 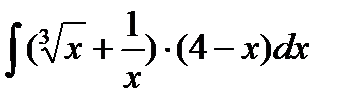 ;
;
б) 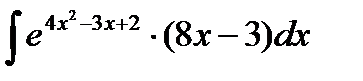 ; б)
; б)  ;
;
в)  ; в)
; в) 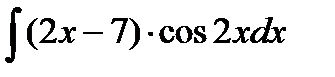 ;
;
3. а)  ; 4. а)
; 4. а)  ;
;
б)  ; б)
; б) 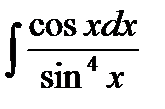 ;
;
в)  ; в)
; в)  ;
;
5. а)  ; 6. а)
; 6. а)  ;
;
б)  ; б)
; б)  ;
;
в)  ; в)
; в)  ;
;
7. а)  ; 8. а)
; 8. а)  ;
;
б)  ; б)
; б)  ;
;
в)  ; в)
; в)  ;
;
9. а)  ; 10. а)
; 10. а)  ;
;
б)  ; б)
; б)  ;
;
в)  ; в)
; в)  ;
;
11. а) 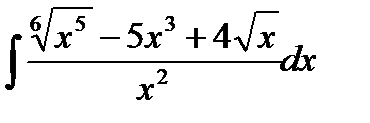 ; 12. а)
; 12. а)  ;
;
б)  ; б)
; б)  ;
;
в)  ; в)
; в)  ;
;
13. а)  ; 14. а)
; 14. а)  ;
;
б)  б)
б)  ;
;
в)  ; в)
; в)  ;
;
15. а)  ; 16. а)
; 16. а)  ;
;
б)  ; б)
; б)  ;
;
в)  ; в)
; в)  ;
;
17. а)  ; 18. а)
; 18. а)  ;
;
б)  ; б)
; б)  ;
;
в)  ; в)
; в)  ;
;
19. а)  ; 20. а)
; 20. а)  ;
;
б)  ; б)
; б) 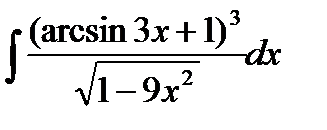 ;
;
в)  ; в)
; в)  .
.
Задачи 21 – 40. Найти неопределённые интегралы:
21. а)  ; б)
; б)  ;
;
22. а)  ; б)
; б)  ;
;
23. а)  ; б)
; б)  ;
;
24. а)  ; б)
; б)  ;
;
25. а) 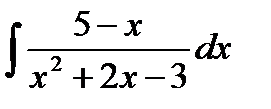 ; б)
; б)  ;
;
26. а)  ; б)
; б)  ;
;
27. а)  ; б)
; б)  ;
;
28. а)  ; б)
; б)  ;
;
29. а)  ; б)
; б)  ;
;
30. а) 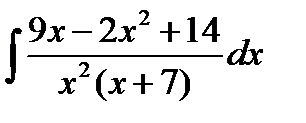 ; б)
; б)  ;
;
31. а)  ; б)
; б)  ;
;
32. а)  ; б)
; б)  ;
;
33. а)  ; б)
; б)  ;
;
34. а)  ; б)
; б)  ;
;
35. а)  ; б)
; б)  ;
;
36. а)  ; б)
; б)  ;
;
37. а)  ; б)
; б)  ;
;
38. а)  ; б)
; б)  ;
;
39. а)  ; б)
; б) 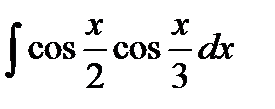 ;
;
40. а) 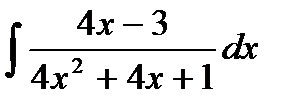 ; б)
; б)  .
.
41. Вычислить объём тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями  ,
,  ,
,  .
.
42. Вычислить площадь фигуры, расположенной в верхней полуплоскости и ограниченной линиями:

43. Вычислить объем тела, образованного вращением вокруг оси ординат фигуры, ограниченной линиями:

44. Вычислить площадь фигуры, ограниченной линиями:

45. Вычислить объем тела, образованного вращением вокруг оси абсцисс фигуры, расположенной в первой четверти и ограниченной линиями:

46. Вычислить площадь фигуры, ограниченной линиями:

47. Криволинейная трапеция, ограниченная линиями:  вращается вокруг оси абсцисс. Вычислить объем тела, которое при этом образуется.
вращается вокруг оси абсцисс. Вычислить объем тела, которое при этом образуется.
48. Вычислить площадь фигуры, ограниченной линиями: 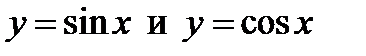 и лежащей между любыми двумя точками пересечения этих кривых.
и лежащей между любыми двумя точками пересечения этих кривых.
49. Вычислить объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями:

50. Найти площадь фигуры, ограниченной линиями:

51. Вычислить объём тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями  ,
,  .
.
52. Вычислить площадь фигуры, расположенной в верхней полуплоскости и ограниченной линиями:

53. Вычислить объем тела, образованного вращением вокруг оси ординат фигуры, ограниченной линиями:

 ;
; 
54. Вычислить площадь фигуры, ограниченной линиями:

55. Вычислить объем тела, образованного вращением вокруг оси абсцисс фигуры, расположенной в первой четверти и ограниченной линиями:


56. Вычислить площадь фигуры, ограниченной линиями:

57. Вычислить объем тела, образованного вращением вокруг оси ординат фигуры, ограниченной линиями:

58. Вычислить объем тела, образованного вращением вокруг оси ординат фигуры, ограниченной линиями:

59. Вычислить объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями:
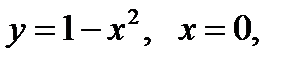


60. Найти площадь фигуры, ограниченной линиями:

Задачи 61 – 70. Вычислить несобственный интеграл или установить его расходимость:
61.  62.
62. 
63.  64.
64. 
65.  66.
66. 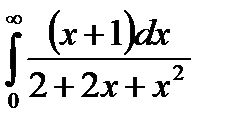
67.  68.
68. 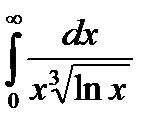
69.  70.
70. 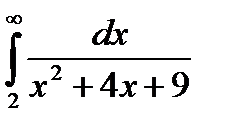
71.  72.
72. 
73.  74.
74. 
75.  76.
76. 
77.  78.
78. 
79.  80.
80. 
Литература.
Основная литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1-2,-М.:Наука, Гл.ред.физ-мат. Лит.,2008,-416с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., Высшая школа, 2004,-542с.
3. Берман Г.Н. Сборник задач по курсу мат. анализа. СП, Профессия, 2003,- 432 с.
4. Привалов И. И.Аналитическая геометрия.М., Наука, 2003-299 с..
Дополнительная литература
1. Гусак А.А.. Сборник задач по аналитической геометрии. Минск.:ТетраСистемс,2008.-288с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая мат-ка в упражнениях и задачах., часть 1-2 М., Мир и образование, 2005.-293с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. М., В.ш., 2003,-403с.
4. Лунгу К.Н.Сборник задач по высшей математике. 1, 2 часть. М., Айрис – пресс, 2009.
5. Письменный Д.Т. Конспект лекций по высшей математике. М., Айрис – пресс, 2008,-256с.
6. Кремер Н.Ш. Теория вероятностей и математическая статистика. М., ЮНИТИ – ДАНА, 2003,-543с.
7. Расчетное задание № 1. Линейная алгебра и аналитическая геометрия. УФА, 2001.
8. Расчетное задание № 2А. Введение в анализ. УФА, 2000.
9. Расчетное задание № 2Б. Дифференцирование функций одной переменной и некоторые приложения дифференциального исчисления. УФА, 2002.
10. Расчетное задание № 3. Неопределенный и определенный интегралы. УФА, 2000.
11. Расчетное задание № 4Б. Элементы векторного анализа. УНИ, 1980.
12. Расчетное задание № 5. Дифференциальные уравнения. УФА, 2002.
13. Расчетное задание № 6. Ряды
14. Расчетное задание № 7. Основы теории вероятностей и математической статистики. УНИ, 1979.
15. Кузнецов Л.А. Сборник заданий по высшей математике и математической статистике. УНИ,1979.
Дата публикования: 2014-11-03; Прочитано: 613 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
