 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лемма о первообразных
|
|
Если F1(x) и F2(x) – две первообразные для функции f(x) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу.
Из этой теоремы следует, что если известна какая-нибудь первообразная F(x) данной функции f(x), то всё множество первообразных для f(x) можно записать в виде F(x)+C.
Выражение F(x)+C, где F(x) – первообразная функции f(x) и С – произвольная постоянная, называется неопределённым интегралом от функции f(x) и обозначается символом 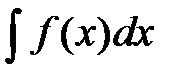 , причём f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением,
, причём f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением,
х – переменной интегрирования; 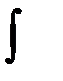 – знак неопределённого интеграла.
– знак неопределённого интеграла.
Таким образом, по определению
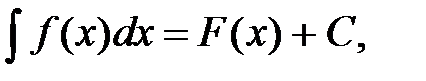
если 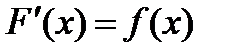 .
.
Возникает вопрос: для всякой ли функции f(x) существует первообразная, а значит, и неопределённый интеграл?
Дата публикования: 2014-11-03; Прочитано: 1349 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
