Степенные ряды

Одним из важных классов функциональных рядов являются степенные ряды.

Определение 6.2.9.Функциональные ряды, членами которых являются целые положительные степени независимой переменной х или двучлена (х-х₀), (где х₀=const), умноженные на числовые коэффициенты:

(1) , или

(2) 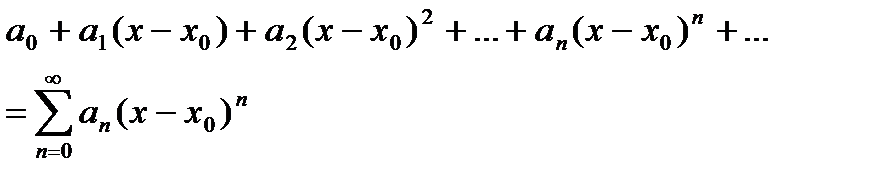называются степенными рядами.

Члены степенных рядов являются: 1) непрерывными и 2) дифференцируемыми функциями на всей числовой оси.

Ряд (1) получается из ряда (2) при х₀=0.

Все последующие рассуждения будем проводить для ряда (1), поскольку ряд (2) приводится к ряду (1) с помощью замены переменной х-х₀=Х.

Замечание 6.2.10. Для удобства n-м членом степенного ряда называют член , несмотря на то, что он стоит на (n+1)-м месте. Свободный член ряда a₀ считают нулевым членом.

Логически могут представиться 3 возможности:

1)ряд (1) сходится на свей числовой оси;

2)ряд сходится только в т. х=0 (в т. х=0 сходится всякий степенной ряд (1),

сумма ряда = a₀)

3) ряд сходится не только в точке х=0, но и не на всей числовой оси.