Цилиндрические и конические поверхности

Займемся теперь изучением поверхностей. Их уравнения после преобразований могут быть приведены к виду , Мы будем предполагать, что есть многочлен относительно Степень этого многочлена относительно определяет порядок алгебраической поверхности. Можно показать, что он не зависит от выбора координатных осей. Ранее мы убедились в том, что поверхностями 1-го порядка являются плоскости. Займемся исследованием поверхностей 2-го порядка.

Начнем с цилиндрической поверхности. Цилиндрической называется поверхность, образованная прямыми, называемыми образующими, параллельными некоторой данной прямой и пересекающими данную линию , которая называется направляющей. Пусть направляющая цилиндрической поверхности определяется уравнениями

(5.31)

а образующие уравнениями

(5.32)

где есть точка, принадлежащая направляющей, а - текущие координаты поверхности. Исключая из четырех уравнений (5.31) и (5.32), получим искомое уравнение цилиндрической поверхности.

Пример 5.13. Составить уравнение цилиндрической поверхности, образующие которой параллельны прямой , а направляющей служит прямая

. Рассмотрим канонические уравнения образующих:

Обозначим через 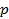величину каждого из этих отношений, тогда , 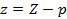. Подставляя эти значения в данные уравнения направляющей, получим: . Исключив 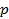, найдем: Это есть уравнение плоскости, проходящей через данную направляющую и параллельной прямой .

Конической называется поверхность, образованная прямыми (образующими конуса), проходящими через данную точку (вершину конуса) и пересекающими данную линию (направляющую конуса).

Пусть направляющая конуса задается уравнениями

, (5.33)

а вершина конуса имеет координаты Канонические уравнения образующих конуса как прямых, проходящих через точку и через точку направляющей, будут:

Исключая из уравнений (5.33) и (5.34), получим искомое уравнение конической поверхности.

Пример 5.14. Составить уравнение конуса с вершиной в начале координат и направляющей

Канонические уравнения образующих, проходящих через вершину (0;0;0) конуса и точку направляющей, будут:

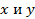Исключим из четырех данных уравнений. Заменяя на c, определим из последних двух уравнений:

Подставляя эти значения 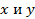в первое уравнение направляющей, будем иметь:

Если в рассмотренном примере 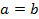, то направляющей будет окружность, и мы получим круговой конус.