| 1. Четная функция
| Функция  , определенная на множестве , определенная на множестве  , называется четной, если для любого значения , называется четной, если для любого значения 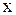 из из  выполняются условия выполняются условия
 и и  .
График четной функции симметричен относительно .
График четной функции симметричен относительно 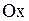 . .
| Задача.
Укажите график четной функции.
Варианты ответов:
1)  2) 2)  3)
3)  4) 4)  Решение.
График четной функции симметричен относительно оси
Решение.
График четной функции симметричен относительно оси  , поэтому рис. №2.
Ответ. №2. , поэтому рис. №2.
Ответ. №2.
|
| 2. Нечетная функция
| Функция  , определенная на множестве , определенная на множестве  , называется нечетной, если для любого значения , называется нечетной, если для любого значения 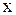 из из  выполняются условия выполняются условия
 и и  .
График нечетной функции симметричен относительно начала координат. .
График нечетной функции симметричен относительно начала координат.
| Задача.
Укажите график нечетной функции.
Варианты ответов:
1)  2) 2)  3)
3)  4) 4)  Решение.
График нечетной функции симметричен относительно начала координат (точки О), поэтому рис. №3.
Ответ. №3.
Решение.
График нечетной функции симметричен относительно начала координат (точки О), поэтому рис. №3.
Ответ. №3.
|
| 3. Периодическая функция
| Функция  , определенная на множестве , определенная на множестве  , называется периодическойна этом множестве, если существует такое число , называется периодическойна этом множестве, если существует такое число  , что при каждом , что при каждом  значение значение 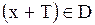 и и  . При этом Т называется периодом функции.
Для построения графика периодической функции периода . При этом Т называется периодом функции.
Для построения графика периодической функции периода  достаточно построить его на любом отрезке длины Т и периодически продолжить его во всю область определения.
Элементарными периодическими функциями являются: достаточно построить его на любом отрезке длины Т и периодически продолжить его во всю область определения.
Элементарными периодическими функциями являются:  , ,  , ,  , , 
| Задача.
Укажите график периодической функции
Варианты ответов:
1)  2) 2)  3)
3)  4) 4)  Ответ. №4.
Задача.
Периодической является функция…
Варианты ответов: 1)
Ответ. №4.
Задача.
Периодической является функция…
Варианты ответов: 1)  2) 2)  3)
3)  4) 4)  Решение.
Функция, описываемая уравнением №3 является периодической.
Ответ. №3.
Решение.
Функция, описываемая уравнением №3 является периодической.
Ответ. №3.
|
| 4. Простые
гармонические колебания
5. Период
колебания
| Колебания, при которых изменения физических величин происходят по закону  или или  , называются простыми гармоническими колебаниями.
А – амплитуда колебания, , называются простыми гармоническими колебаниями.
А – амплитуда колебания,
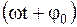 - фаза колебания, - фаза колебания,
 - частота колебания, - частота колебания,
 - начальная фаза. - начальная фаза.

| Задача.
Гармонические колебания с амплитудой равной 5, частотой равной 3 и начальной фазой  описываются законом…
Решение. описываются законом…
Решение.
 Задача.
Гармонические колебания с амплитудой D, частотой
Задача.
Гармонические колебания с амплитудой D, частотой  и начальной фазой и начальной фазой  определяются уравнением…
Варианты ответов:
1) определяются уравнением…
Варианты ответов:
1)  2) 2)  3)
3)  4) 4)  Ответ. №4.
Ответ. №4.
|
6. Ряд Фурье функции 
| Рядом Фурье периодической функции  с периодом с периодом  , определенной на отрезке , определенной на отрезке  , называется функциональный ряд , называется функциональный ряд
 ,
где ,
где  , ,
 , ,
 , ,  Величина интегралов в данных формулах не изменится, если пределами их взять
Величина интегралов в данных формулах не изменится, если пределами их взять  и и  .
Тогда: .
Тогда:

 , ,
 , , 
| Задача.
График функции  при при  и его периодическое продолжение заданы на рисунке и его периодическое продолжение заданы на рисунке
 Тогда ряд Фурье для этой функции имеет вид…
Варианты ответов: 1)
Тогда ряд Фурье для этой функции имеет вид…
Варианты ответов: 1)  2)
2)  3)
3)  4) 4)  Решение.
По рисунку видно, что функция
Решение.
По рисунку видно, что функция  - общего вида, поэтому ряд Фурье для нее имеет вид №3.
Ответ. №3. - общего вида, поэтому ряд Фурье для нее имеет вид №3.
Ответ. №3.
|
| 7. Ряд Фурье для четной функции
| Ряд Фурье для четной функции содержит только свободный член и косинусы, т.е.
 , где , где
 , ,
 , ,
 , , 
| Задача.
Функция 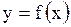 , заданная на отрезке , заданная на отрезке  является четной. Тогда разложение этой функции в ряд Фурье может иметь вид…
Варианты ответов:
1) является четной. Тогда разложение этой функции в ряд Фурье может иметь вид…
Варианты ответов:
1)  2)
2)  3)
3)  4)
4)  Решение.
Т.к.
Решение.
Т.к. 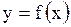 является четной функцией, то является четной функцией, то  . Поэтому разложение этой функции в ряд Фурье может иметь вид 4.
Ответ. №4. . Поэтому разложение этой функции в ряд Фурье может иметь вид 4.
Ответ. №4.
|
| 8. Ряд Фурье для нечетной функции
| Ряд Фурье для нечетной функции состоит только из синусов
 , где , где  , ,  , ,
 , , 
| Задача.
Дана функция  , ,  . Тогда коэффициент . Тогда коэффициент 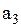 разложения разложения  в ряд Фурье равен…
Решение.
Функция в ряд Фурье равен…
Решение.
Функция  является нечетной, поэтому коэффициент является нечетной, поэтому коэффициент  равен 0. Следовательно, равен 0. Следовательно,  .
Ответ. 0. .
Ответ. 0.
|
9. Условия
Дирихле (разложения функции  в ряд Фурье) в ряд Фурье)
| 1) функция  должна быть непрерывной в промежутке значения х от должна быть непрерывной в промежутке значения х от  до до  или может иметь в указанном промежутке конечное число разрывов первого рода.
2) функция или может иметь в указанном промежутке конечное число разрывов первого рода.
2) функция  должна иметь конечное число максимумов и минимумов или не иметь их совсем. должна иметь конечное число максимумов и минимумов или не иметь их совсем.
|
| 10. Теорема
Дирихле
| Если функция  с областью существования с областью существования  удовлетворяет условиям Дирихле, то
1) ряд Фурье функции удовлетворяет условиям Дирихле, то
1) ряд Фурье функции  сходится в указанном промежутке значений х;
2) сумма этого ряда равна функции сходится в указанном промежутке значений х;
2) сумма этого ряда равна функции  во всех точках ее непрерывности;
3) в каждой точке разрыва функции сумма ряда равна величине ординаты средней точки скачка графика функции;
4) при во всех точках ее непрерывности;
3) в каждой точке разрыва функции сумма ряда равна величине ординаты средней точки скачка графика функции;
4) при  и и  сумма ряда одинакова и равна сумма ряда одинакова и равна
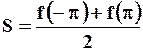 . .
| Задача.
График периодической функции имеет вид:

 - сумма ряда Фурье для этой функции. Тогда сумма - сумма ряда Фурье для этой функции. Тогда сумма  равна…
Решение.
В точке равна…
Решение.
В точке  функция функция  терпит разрыв, поэтому терпит разрыв, поэтому
 .
Ответ. .
Ответ.  . .
|
| | | | |

 , определенная на множестве
, определенная на множестве  , называется четной, если для любого значения
, называется четной, если для любого значения 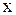 из
из  выполняются условия
выполняются условия
 и
и  .
График четной функции симметричен относительно
.
График четной функции симметричен относительно 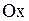 .
.
 2)
2)  3)
3)  4)
4)  Решение.
График четной функции симметричен относительно оси
Решение.
График четной функции симметричен относительно оси  , поэтому рис. №2.
Ответ. №2.
, поэтому рис. №2.
Ответ. №2.
 , определенная на множестве
, определенная на множестве  , называется нечетной, если для любого значения
, называется нечетной, если для любого значения 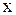 из
из  выполняются условия
выполняются условия
 и
и  .
График нечетной функции симметричен относительно начала координат.
.
График нечетной функции симметричен относительно начала координат.
 2)
2)  3)
3)  4)
4)  Решение.
График нечетной функции симметричен относительно начала координат (точки О), поэтому рис. №3.
Ответ. №3.
Решение.
График нечетной функции симметричен относительно начала координат (точки О), поэтому рис. №3.
Ответ. №3.
 , определенная на множестве
, определенная на множестве  , называется периодическойна этом множестве, если существует такое число
, называется периодическойна этом множестве, если существует такое число  , что при каждом
, что при каждом  значение
значение 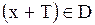 и
и  . При этом Т называется периодом функции.
Для построения графика периодической функции периода
. При этом Т называется периодом функции.
Для построения графика периодической функции периода  достаточно построить его на любом отрезке длины Т и периодически продолжить его во всю область определения.
Элементарными периодическими функциями являются:
достаточно построить его на любом отрезке длины Т и периодически продолжить его во всю область определения.
Элементарными периодическими функциями являются:  ,
,  ,
,  ,
, 
 2)
2)  3)
3)  4)
4)  Ответ. №4.
Задача.
Периодической является функция…
Варианты ответов: 1)
Ответ. №4.
Задача.
Периодической является функция…
Варианты ответов: 1)  2)
2)  3)
3)  4)
4)  Решение.
Функция, описываемая уравнением №3 является периодической.
Ответ. №3.
Решение.
Функция, описываемая уравнением №3 является периодической.
Ответ. №3.
 или
или  , называются простыми гармоническими колебаниями.
А – амплитуда колебания,
, называются простыми гармоническими колебаниями.
А – амплитуда колебания,
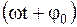 - фаза колебания,
- фаза колебания,
 - частота колебания,
- частота колебания,
 - начальная фаза.
- начальная фаза.

 описываются законом…
Решение.
описываются законом…
Решение.
 Задача.
Гармонические колебания с амплитудой D, частотой
Задача.
Гармонические колебания с амплитудой D, частотой  и начальной фазой
и начальной фазой  определяются уравнением…
Варианты ответов:
1)
определяются уравнением…
Варианты ответов:
1)  2)
2)  3)
3)  4)
4)  Ответ. №4.
Ответ. №4.

 с периодом
с периодом  , определенной на отрезке
, определенной на отрезке  , называется функциональный ряд
, называется функциональный ряд
 ,
где
,
где  ,
,
 ,
,
 ,
,  Величина интегралов в данных формулах не изменится, если пределами их взять
Величина интегралов в данных формулах не изменится, если пределами их взять  и
и  .
Тогда:
.
Тогда:

 ,
,
 ,
, 
 при
при  и его периодическое продолжение заданы на рисунке
и его периодическое продолжение заданы на рисунке
 Тогда ряд Фурье для этой функции имеет вид…
Варианты ответов: 1)
Тогда ряд Фурье для этой функции имеет вид…
Варианты ответов: 1)  2)
2)  3)
3)  4)
4)  Решение.
По рисунку видно, что функция
Решение.
По рисунку видно, что функция  - общего вида, поэтому ряд Фурье для нее имеет вид №3.
Ответ. №3.
- общего вида, поэтому ряд Фурье для нее имеет вид №3.
Ответ. №3.
 , где
, где
 ,
,
 ,
,
 ,
, 
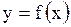 , заданная на отрезке
, заданная на отрезке  является четной. Тогда разложение этой функции в ряд Фурье может иметь вид…
Варианты ответов:
1)
является четной. Тогда разложение этой функции в ряд Фурье может иметь вид…
Варианты ответов:
1)  2)
2)  3)
3)  4)
4)  Решение.
Т.к.
Решение.
Т.к. 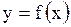 является четной функцией, то
является четной функцией, то  . Поэтому разложение этой функции в ряд Фурье может иметь вид 4.
Ответ. №4.
. Поэтому разложение этой функции в ряд Фурье может иметь вид 4.
Ответ. №4.
 , где
, где  ,
,  ,
,
 ,
, 
 ,
,  . Тогда коэффициент
. Тогда коэффициент 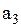 разложения
разложения  в ряд Фурье равен…
Решение.
Функция
в ряд Фурье равен…
Решение.
Функция  является нечетной, поэтому коэффициент
является нечетной, поэтому коэффициент  равен 0. Следовательно,
равен 0. Следовательно,  .
Ответ. 0.
.
Ответ. 0.
 в ряд Фурье)
в ряд Фурье)
 должна быть непрерывной в промежутке значения х от
должна быть непрерывной в промежутке значения х от  до
до  или может иметь в указанном промежутке конечное число разрывов первого рода.
2) функция
или может иметь в указанном промежутке конечное число разрывов первого рода.
2) функция  должна иметь конечное число максимумов и минимумов или не иметь их совсем.
должна иметь конечное число максимумов и минимумов или не иметь их совсем.
 с областью существования
с областью существования  удовлетворяет условиям Дирихле, то
1) ряд Фурье функции
удовлетворяет условиям Дирихле, то
1) ряд Фурье функции  сходится в указанном промежутке значений х;
2) сумма этого ряда равна функции
сходится в указанном промежутке значений х;
2) сумма этого ряда равна функции  во всех точках ее непрерывности;
3) в каждой точке разрыва функции сумма ряда равна величине ординаты средней точки скачка графика функции;
4) при
во всех точках ее непрерывности;
3) в каждой точке разрыва функции сумма ряда равна величине ординаты средней точки скачка графика функции;
4) при  и
и  сумма ряда одинакова и равна
сумма ряда одинакова и равна
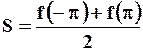 .
.

 - сумма ряда Фурье для этой функции. Тогда сумма
- сумма ряда Фурье для этой функции. Тогда сумма  равна…
Решение.
В точке
равна…
Решение.
В точке  функция
функция  терпит разрыв, поэтому
терпит разрыв, поэтому
 .
Ответ.
.
Ответ.  .
.
