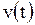3. Формула интегрирования по частям

| Задача.
Вычислить интеграл  .
Решение. .
Решение.
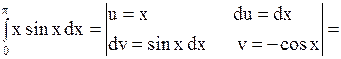 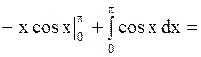
 .
Ответ. .
Ответ.  . .
|
|
4. Интегрирование четных и нечетных функций в симметричных пределах

|
|
Задача.
Вычислить интеграл  .
Решение. .
Решение.
  .
Ответ. 0. .
Ответ. 0.
| Задача.
Вычислить интеграл  .
Решение. .
Решение.
   .
Ответ. .
Ответ.  . .
|
|
| §2 Несобственные интегралы
|
|
| Несобственные интегралы I рода
|
|
Если функция  непрерывна на непрерывна на  , то , то
 (*)
Если функция (*)
Если функция  непрерывна на непрерывна на  , то , то
 (**)
Если функция (**)
Если функция  непрерывна на непрерывна на  , то , то
  (***)
Если пределы (*), (**) существуют и конечны, то несобственный интеграл – сходящийся, если эти пределы не существуют или бесконечны - расходящийся.
Интеграл сходится – если сходится каждый из двух интегралов в равенстве (***). (***)
Если пределы (*), (**) существуют и конечны, то несобственный интеграл – сходящийся, если эти пределы не существуют или бесконечны - расходящийся.
Интеграл сходится – если сходится каждый из двух интегралов в равенстве (***).
| Задача.
Вычислить несобственный интеграл или установить его расходимость:  .
Решение. .
Решение.

 , интеграл сходится. , интеграл сходится.
|
|
| Несобственные интегралы II рода
|
|
Если  - непрерывна на - непрерывна на  и имеет бесконечный разрыв при и имеет бесконечный разрыв при  , то , то
 . (*)
Если функция . (*)
Если функция  терпит бесконечный разрыв в точке терпит бесконечный разрыв в точке  , то , то
 . (**)
Если . (**)
Если  терпит бесконечный разрыв внутри отрезка терпит бесконечный разрыв внутри отрезка  , т.е. в точке , т.е. в точке  , ,  , то , то
 . (***)
Если пределы (*), (**) существуют и конечны, то несобственный интеграл – сходящийся, если эти пределы не существуют или бесконечны - расходящийся.
Интеграл сходится – если сходится каждый из двух интегралов в равенстве (***). . (***)
Если пределы (*), (**) существуют и конечны, то несобственный интеграл – сходящийся, если эти пределы не существуют или бесконечны - расходящийся.
Интеграл сходится – если сходится каждый из двух интегралов в равенстве (***).
| Задача.
Вычислить несобственный интеграл или установить его расходимость:  Решение.
Решение.

 , интеграл расходится. , интеграл расходится.
|
|
| §3 Геометрические приложения определенного интеграла
|
|
| Площадь плоской фигуры в декартовой системе координат
| Площадь плоской фигуры в полярной системе координат
|
|
 , , 
 
|
 - непрерывна на - непрерывна на  , , 


|
|
Задача.
 Площадь фигуры, ограниченной параболой Площадь фигуры, ограниченной параболой  и прямой и прямой  , вычисляется с помощью интеграла…
Варианты ответов: 1) , вычисляется с помощью интеграла…
Варианты ответов: 1) 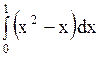 2) 2)  3) 3)  4)
4) 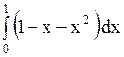 Решение.
Решение.
 , следовательно, , следовательно, 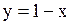 .
На отрезке .
На отрезке  график функции график функции  расположен выше графика функции расположен выше графика функции 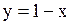 , поэтому , поэтому
  Ответ. №3.
Ответ. №3.
|
|
| Длина дуги плоской кривой в декартовой системе координат
| 
 , , 
| Задача.
Найти длину дуги кривой  от от  до до   .
Решение.
Так как .
Решение.
Так как  , то , то  ; ;  . .
 . .


 .
Ответ. .
Ответ.  . .
|
|

 , , 
|
|
| Длина дуги плоской кривой в полярной системе координат
|

 , , 
|
|
| Длина дуги плоской кривой в параметрическом виде на плоскости
|

 
|
|
| Длина дуги плоской кривой в параметрическом виде в пространстве
|

 
|
|
|
|
| Объем
| Площадь поверхности
|
Объем и площадь поверхности тела вращения
Кривая  , ,  вращается вокруг оси вращается вокруг оси  Кривая
Кривая  , ,  вращается вокруг оси вращается вокруг оси 
|  
|


|


|
| §4 Применение определенного интеграла к решению некоторых задач физики
|
| Вычисление работы
| Вычисление работы переменной силы  , при перемещении точки вдоль оси , при перемещении точки вдоль оси  из положения из положения  в положение в положение 
| 
|
| Вычисление пути
| Путь пройденный телом за промежуток времени от  до до  со скоростью со скоростью 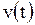
| 
|
| | | | | | | | | | | | | | | |


 .
Решение.
.
Решение.
 .
Ответ. 9.
.
Ответ. 9.
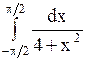 .
Решение.
.
Решение.
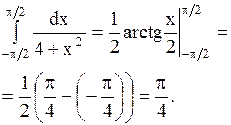 Ответ.
Ответ.  .
.
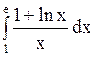 .
Решение.
.
Решение.

 .
Ответ.
.
Ответ.  .
.

 .
Решение.
.
Решение.
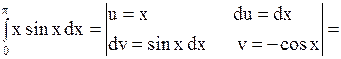
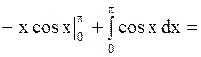
 .
Ответ.
.
Ответ.  .
.

 .
Решение.
.
Решение.

 .
Ответ. 0.
.
Ответ. 0.
 .
Решение.
.
Решение.


 .
Ответ.
.
Ответ.  .
.
 непрерывна на
непрерывна на  , то
, то
 (*)
Если функция
(*)
Если функция  непрерывна на
непрерывна на  , то
, то
 (**)
Если функция
(**)
Если функция  непрерывна на
непрерывна на  , то
, то

 (***)
Если пределы (*), (**) существуют и конечны, то несобственный интеграл – сходящийся, если эти пределы не существуют или бесконечны - расходящийся.
Интеграл сходится – если сходится каждый из двух интегралов в равенстве (***).
(***)
Если пределы (*), (**) существуют и конечны, то несобственный интеграл – сходящийся, если эти пределы не существуют или бесконечны - расходящийся.
Интеграл сходится – если сходится каждый из двух интегралов в равенстве (***).
 .
Решение.
.
Решение.

 , интеграл сходится.
, интеграл сходится.
 - непрерывна на
- непрерывна на  и имеет бесконечный разрыв при
и имеет бесконечный разрыв при  , то
, то
 . (*)
Если функция
. (*)
Если функция  терпит бесконечный разрыв в точке
терпит бесконечный разрыв в точке  , то
, то
 . (**)
Если
. (**)
Если  терпит бесконечный разрыв внутри отрезка
терпит бесконечный разрыв внутри отрезка  , т.е. в точке
, т.е. в точке  ,
,  , то
, то
 . (***)
Если пределы (*), (**) существуют и конечны, то несобственный интеграл – сходящийся, если эти пределы не существуют или бесконечны - расходящийся.
Интеграл сходится – если сходится каждый из двух интегралов в равенстве (***).
. (***)
Если пределы (*), (**) существуют и конечны, то несобственный интеграл – сходящийся, если эти пределы не существуют или бесконечны - расходящийся.
Интеграл сходится – если сходится каждый из двух интегралов в равенстве (***).
 Решение.
Решение.

 , интеграл расходится.
, интеграл расходится.
 ,
, 


 - непрерывна на
- непрерывна на  ,
, 


 Площадь фигуры, ограниченной параболой
Площадь фигуры, ограниченной параболой  и прямой
и прямой  , вычисляется с помощью интеграла…
Варианты ответов: 1)
, вычисляется с помощью интеграла…
Варианты ответов: 1) 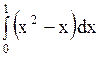 2)
2)  3)
3)  4)
4)  Решение.
Решение.
 , следовательно,
, следовательно, 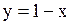 .
На отрезке
.
На отрезке  график функции
график функции  расположен выше графика функции
расположен выше графика функции 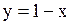 , поэтому
, поэтому

 Ответ. №3.
Ответ. №3.

 ,
, 
 от
от  до
до 
 .
Решение.
Так как
.
Решение.
Так как  , то
, то  ;
;  .
.
 .
.


 .
Ответ.
.
Ответ.  .
.

 ,
, 

 ,
, 






 ,
,  вращается вокруг оси
вращается вокруг оси  Кривая
Кривая  ,
,  вращается вокруг оси
вращается вокруг оси 






 , при перемещении точки вдоль оси
, при перемещении точки вдоль оси  из положения
из положения  в положение
в положение 

 до
до  со скоростью
со скоростью