 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Глава 9. Предел функции в точке
|
|
Если функция  в точке
в точке  непрерывна, то
непрерывна, то  . Т.е. для вычисления предела в функцию подставляется то значение х, к которому приближается эта переменная.
. Т.е. для вычисления предела в функцию подставляется то значение х, к которому приближается эта переменная.
Например,  .
.
| §1 Некоторые неопределенности и правила их раскрытия | ||||||
1. Неопределенность вида

|  , ,  - многочлены - многочлены
 - максимальная степень числителя; - максимальная степень числителя;
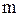 - максимальная степень знаменателя. - максимальная степень знаменателя.
 где
где  - коэффициент при max степени числителя - коэффициент при max степени числителя
 - коэффициент при max степени знаменателя - коэффициент при max степени знаменателя
| Задача.
Значение предела  равно…
1) 2 2) 1 3) 0 4) равно…
1) 2 2) 1 3) 0 4)  Решение.
Максимальные степени числителя и знаменателя совпадают (=2). Коэффициент при max степени числителя =2, в знаменателе = 1.
Решение.
Максимальные степени числителя и знаменателя совпадают (=2). Коэффициент при max степени числителя =2, в знаменателе = 1.
 Ответ. №1
Задача.
Ответ. №1
Задача.
 Решение.
Максимальная степень числителя =3, знаменателя = 2 (3>2). Следовательно,
Решение.
Максимальная степень числителя =3, знаменателя = 2 (3>2). Следовательно,
 Ответ.
Ответ.  . .
| ||||
2. Неопределенность вида

|
Числитель и знаменатель раскладывается на множители с использованием формул:
1)  2)
2)  3)
3)  4)
4) 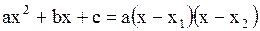 , где , где
 - корни уравнения - корни уравнения 
| Задача.
 Решение.
Решение.
 Разложим числитель и знаменатель на множители:
1)
Разложим числитель и знаменатель на множители:
1)  2)
2) 

 ; ;  . .
 .
Тогда .
Тогда  Ответ.
Ответ.  . .
| ||||
3. Неопределенность вида

| Если в функции есть выражение вида  , то числитель и знаменатель умножается на , то числитель и знаменатель умножается на  . Если есть выражение вида . Если есть выражение вида  - то на - то на  . .
| Задача. 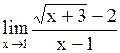 Решение.
Решение.

 Ответ.
Ответ.  . .
| ||||
4. Неопределенность вида

| С использованием эквивалентностей
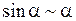 , при , при 
 , при , при 
 , при , при 
 , при , при 
 , при , при 
 , при , при 
 , при , при 
| Задача.
Значение предела  равно…
1) 0 2) равно…
1) 0 2)  3) 3)  4) 1
Решение.
У функции 4) 1
Решение.
У функции  аргумент аргумент 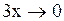 при при  . Можно воспользоваться предложенной эквивалентностью . Можно воспользоваться предложенной эквивалентностью
 Ответ. №2
Ответ. №2
| ||||
5. Неопределенность вида

| Привести две дроби к общему знаменателю. В результате получится неопределенность вида 
| Задача.
 Решение.
Каждая дробь имеет степень числителя больше, чем степень знаменателя. Следовательно, каждая дробь стремится к
Решение.
Каждая дробь имеет степень числителя больше, чем степень знаменателя. Следовательно, каждая дробь стремится к  . .
 Ответ. -10
Ответ. -10
| ||||
| 6. Правило Лопиталя | Правило Лопиталя используется при неопределенностях  или или 

| Задача.
 Решение.
Решение.
 Ответ.
Ответ. 
| ||||
| §2 Непрерывность функции в точке | ||||||
| 1. Точка разрыва I рода (скачок) |  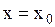 - точка разрыва I рода (скачок), если - точка разрыва I рода (скачок), если 
| Задача.
При каких значениях параметра а функция непрерывна?
 Решение.
Решение.



 Функция непрерывна, если
Функция непрерывна, если  , ,  Ответ.
Ответ.  . .
| ||||
| 2. Точка устранимого разрыва |  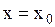 - точка устранимого разрыва(точка разрыва I рода), если - точка устранимого разрыва(точка разрыва I рода), если 
| |||||
| 3. Точка непрерывности |   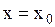 - точка непрерывности, если - точка непрерывности, если
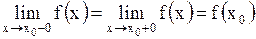
| |||||
| 4. Точка разрыва II рода |  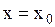 - точка разрыва II рода, если хотя бы один из пределов равен - точка разрыва II рода, если хотя бы один из пределов равен 
 или или 
| |||||
Дата публикования: 2014-11-02; Прочитано: 407 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
