 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Глава 8. Дифференциальная геометрия
|
|
| §1 Уравнение касательной и нормали к кривой | ||||||
Для кривой  в точке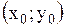 
| Для кривой  в точке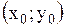
| Для кривой 
| Для кривой 
| |||
| 1. Уравнение касательной | 
| 
| 
| - | ||
| 2. Уравнение нормали | 
| 
| 
| - | ||
| §2 Кривизна кривой | ||||||
| 3. Кривизна для кривой
| 
| Задача.
Кривизна линии  в точке  равна…
Варианты ответов: 1)  2)  3)  4) 
Решение.
Воспользуемся предложенной формулой ;  ;  .
Подставим в полученные производные координаты точки , тогда  ,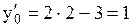 
Ответ. №3.
| ||||
| 4. Кривизна для кривой
| 
| |||||
| 5. Кривизна для кривой
| 
| |||||
| 6. Кривизна для кривой
| 
| |||||
| 7. Радиус кривизны | Радиус кривизны вычисляется по формуле  , где k – кривизна
| Представление о знаке кривизны дает рисунок
| ||||
| §3 Поверхность | |||
| . Уравнение касательной плоскости | Уравнение касательной плоскости к поверхности  в точке 
|
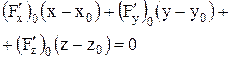
| Задача.
Уравнение касательной плоскости к поверхности  в точке 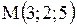 имеет вид…
Варианты ответов:
1)  2) 
3)  4) 
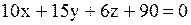Решение.
Найдем частные производные
 ;  ; 
Подставим координаты точки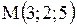
 ;  ; 
Уравнение касательной плоскости примет вид
 
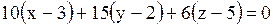
Ответ. №2.
|
Уравнение касательной плоскостик поверхности  в точке
|
| ||
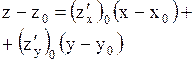
| 9. Уравнение нормали | Уравнение нормалиплоскости к поверхности в точке
| 
| |
| Уравнение нормали к поверхности в точке
| 
|
Дата публикования: 2014-11-02; Прочитано: 357 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
