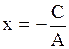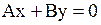|
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Глава 3. Прямая на плоскости
|
|
| §1 Виды уравнений прямой на плоскости | ||
| 1. Уравнение прямой, проходящей через точку с нормальным вектором | 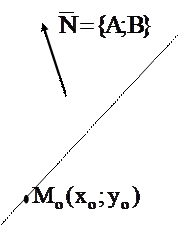 Уравнение прямой, проходящей через точку
Уравнение прямой, проходящей через точку 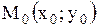 с нормальным вектором с нормальным вектором 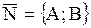 (нормальный вектор – вектор, перпендикулярный прямой)
(нормальный вектор – вектор, перпендикулярный прямой)
| Задача.
Даны вершины треугольника 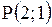 , , 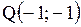 , , 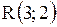 . Тогда уравнение высоты . Тогда уравнение высоты 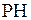 имеет вид…
Варианты ответов: 1) имеет вид…
Варианты ответов: 1) 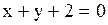 2) 2) 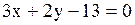 3)
3) 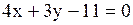 4) 4) 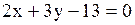 Решение.
Решение.
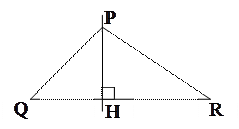 Вектор
Вектор 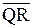 перпендикулярен прямой PH. Тогда перпендикулярен прямой PH. Тогда 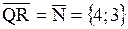 .
Прямая PH проходит через точку .
Прямая PH проходит через точку 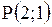 .
Тогда уравнение PH: .
Тогда уравнение PH: 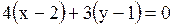 ; ;
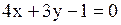 .
Ответ. №3 .
Ответ. №3
|
| 2. Общее уравнение прямой | Общее уравнение прямой
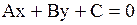 ,
где ,
где 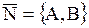 - координаты нормального вектора. - координаты нормального вектора.
| Задача.
Найти нормальный вектор прямой 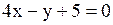 .
Решение.
Коэффициенты при переменных – это координаты нормального вектора. .
Решение.
Коэффициенты при переменных – это координаты нормального вектора. 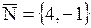 . .
|
| 3. Уравнение прямой в отрезках | 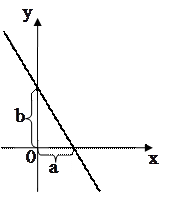  Уравнение прямой в отрезках
Уравнение прямой в отрезках 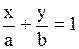
| |
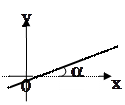
| 4. Уравнение прямой с угловым коэффициентом |
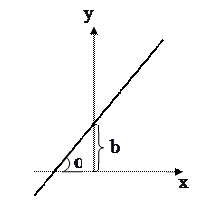 Уравнение прямой с угловым коэффициентом
Уравнение прямой с угловым коэффициентом
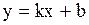
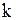 - угловой коэффициент, - угловой коэффициент, 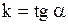
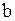 - отрезок, отсекаемый прямой на оси - отрезок, отсекаемый прямой на оси  . .
| Задача.
Прямая проходит через точки 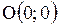 и и 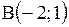 . Тогда ее угловой коэффициент равен…
Решение.
Уравнение прямой через две точки . Тогда ее угловой коэффициент равен…
Решение.
Уравнение прямой через две точки
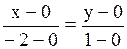 ; ; 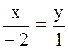 .
Выразим y через x, тогда .
Выразим y через x, тогда
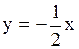 .
Следовательно, .
Следовательно, 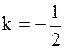
|
| 5. Уравнение прямой, проходящей через точку с направляющим вектором |
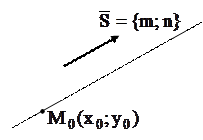 Уравнение прямой, проходящей через точку
Уравнение прямой, проходящей через точку 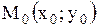 с направляющим вектором с направляющим вектором 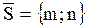
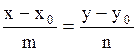 (направляющий вектор – вектор, параллельный прямой)
(направляющий вектор – вектор, параллельный прямой)
| Задача.
Написать уравнение прямой, проходящей через точки 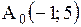 параллельно вектору параллельно вектору 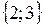 Решение.
Решение.
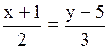
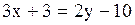
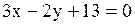
|
| 6. Уравнение прямой, проходящей через две точки | 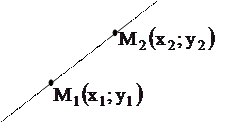 Уравнение прямой, проходящей через две точки
Уравнение прямой, проходящей через две точки 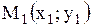 и и 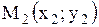
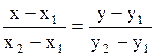
| Задача.
Написать уравнение прямой, проходящей через точки 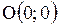 и и 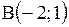 .
Решение. .
Решение.
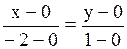
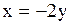 .
Ответ. .
Ответ. 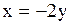 . .
|
| 7. Уравнение прямой по точке с угловым коэффициентом |
Уравнение прямой по точке
Если | Задача.
Градусная мера угла между прямой 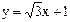 и положительным направлением оси и положительным направлением оси  равна…
Варианты ответов: 1) равна…
Варианты ответов: 1) 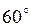 2) 2) 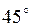 3) 3) 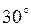 4) 4) 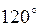 Решение.
Угол между прямой и положительным направлением оси
Решение.
Угол между прямой и положительным направлением оси  находится из углового коэффициента k. находится из углового коэффициента k.
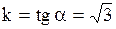 , , 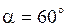 . Ответ. №1.
Задача.
Прямая образует с осью . Ответ. №1.
Задача.
Прямая образует с осью  угол угол 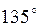 и проходит через точку и проходит через точку 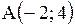 . Написать ее уравнение.
Решение. . Написать ее уравнение.
Решение.
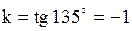 . Подставим k и координаты точки А в уравнение . Подставим k и координаты точки А в уравнение 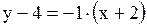 ; ; 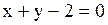 . .
| |||
| 8. Параметрические уравнения прямой |
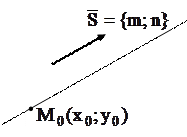   Параметрическиеуравнения прямой
Параметрическиеуравнения прямой
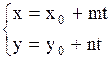
| Задача.
Параметрическими уравнениями прямой на плоскости являются уравнения…
Варианты ответов: 1) 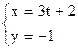 2)
2) 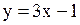 3) 3) 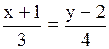 4) 4) 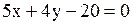 Решение.
Сравнивая варианты ответов и вид параметрических уравнений, приходим к выводу
Ответ. №1.
Решение.
Сравнивая варианты ответов и вид параметрических уравнений, приходим к выводу
Ответ. №1.
| |||
| 9. Расстояние от точки до прямой | Расстояние от точки 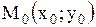 до прямой до прямой 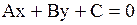 вычисляется по формуле вычисляется по формуле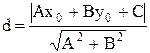
|
| §2 Частные случаи общего уравнения прямой на плоскости | ||||
| 10. Уравнение оси Ох |
ось Ох: | Задача.
Укажите правильное соответствие между уравнениями и типами уравнений прямой
1) 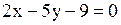 2)
2) 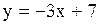 3)
3) 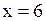 Варианты ответов:
А) уравнение прямой с угловым коэффициентом
В) уравнение прямой, параллельной оси абсцисс
С) общее уравнение прямой
D) уравнение прямой, параллельной оси ординат
Е) уравнение прямой в отрезках на осях
Решение.
Проанализируем все уравнения
1. Уравнение вида
Варианты ответов:
А) уравнение прямой с угловым коэффициентом
В) уравнение прямой, параллельной оси абсцисс
С) общее уравнение прямой
D) уравнение прямой, параллельной оси ординат
Е) уравнение прямой в отрезках на осях
Решение.
Проанализируем все уравнения
1. Уравнение вида 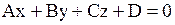 . Это общее уравнение прямой.
2. Это уравнение вида . Это общее уравнение прямой.
2. Это уравнение вида 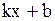 . Это уравнение с угловым коэффициентом.
3. . Это уравнение с угловым коэффициентом.
3. 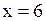 . В уравнении нет переменной . В уравнении нет переменной 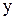 . Тогда прямая параллельна оси . Тогда прямая параллельна оси  .
Ответ. .
Ответ. 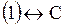 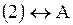 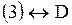 
| ||
| 11. Уравнение оси Оy |
ось Оy: | |||
| 12. Уравнение прямой, параллельной оси Ох |
(в уравнении отсутствует координата | |||
| 13. Уравнение прямой, параллельной оси Оy |
(в уравнении отсутствует координата | |||
| 14. Уравнение прямой, проходящей через начало координат |
Прямая проходит через начало координат:
|
| §3 Взаимное расположение прямых на плоскости | |||
| Вид уравнения прямой | С угловым коэффициентом


| Общее уравнение

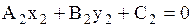
| С направляющим вектором


|
| 15. Условие параллельности прямых | 
| 
| 
|
| 16. Условие перпендикулярности прямых | 
| 
| 
|
| 17. Угол между прямыми | 
| 
| 
|
Задача.
Уравнением прямой, перпендикулярной прямой  , является…
Варианты ответов: 1) , является…
Варианты ответов: 1)  2) 2)  3) 3)  4) 4)  Решение.
Для прямой
Решение.
Для прямой  угловой коэффициент угловой коэффициент  , т.к. прямая должна быть перпендикулярной, то , т.к. прямая должна быть перпендикулярной, то  1)
1)  , ,  , ,  , ,  2)
2)  , ,  , , 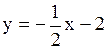 , , 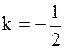 3)
3)  , ,  , ,  4)
4)  , ,  , , 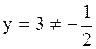 Ответ. №2.
Задача.
Среди прямых, заданных уравнениями
Ответ. №2.
Задача.
Среди прямых, заданных уравнениями  , ,  , ,  , ,  , число неупорядоченных взаимно перпендикулярных пар прямых, равно…
Решение.
Для , число неупорядоченных взаимно перпендикулярных пар прямых, равно…
Решение.
Для 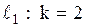 ; ;
 ; ;
 , ,  , , 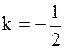 ; ;
 , ,  , , 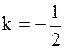 . .
 ; ;  ; ;  ; ;  , т.к. , т.к.  .
Ответ. число неупорядоченных взаимно перпендикулярных пар прямых равно 4. .
Ответ. число неупорядоченных взаимно перпендикулярных пар прямых равно 4.
|
Дата публикования: 2014-11-02; Прочитано: 792 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

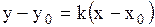 , где
, где 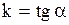
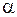 - угол наклона прямой к положительному направлению оси
- угол наклона прямой к положительному направлению оси 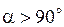 , то
, то 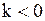 .
.
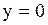
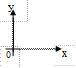
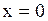
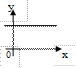
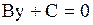 или
или 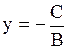
 )
)
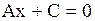 или
или