 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Интегрирование оригинала
|
|
Если функция 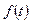 является оригиналом, причем
является оригиналом, причем  , то
, то 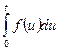 также является оригиналом и
также является оригиналом и
 .
.
Условия 1 и 2 определения оригинала для 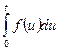 очевидно, выполняются. Выполняется и условие 3, ибо
очевидно, выполняются. Выполняется и условие 3, ибо

Таким образом, 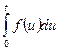 действительно является оригиналом, и мы получаем
действительно является оригиналом, и мы получаем

 ,
,
ибо формула (2.10) применима, так как 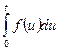 =0 при
=0 при  .
.
Деление равенства (2.9) на  дает требуемое. Таким образом, интегрирование оригинала сводится к делению его изображения на
дает требуемое. Таким образом, интегрирование оригинала сводится к делению его изображения на  .
.
Пример 8. Так как 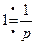 ,
,  , то
, то

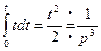
…………………….
 ,
,
или
 ,
,
что является частным случаем соотношения (2.15) при 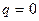 .
.
Дата публикования: 2014-11-02; Прочитано: 520 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
