Интегрирование изображений

Если является оригиналом (тогда 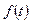тоже оригинал), то из условия следует , где .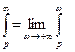

Пусть 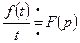, тогда по правилу дифференцирования изображения

,

следовательно, . (2.16)

Интегрируя равенство (2.16) в пределах от до , будем иметь:

,

следовательно, переходя к пределу при и учитывая следствие из теоремы 2.1, получим

, то есть .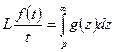

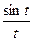Пример 9. Так как , то замечая, что также является оригиналом (ибо ), то по правилу интегрирования изображения имеем

.

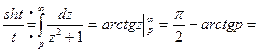
Пример 10. Так как , замечая, что также является оригиналом

(ибо ), то по правилу интегрирования изображения имеем

.