 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие свертки. Теорема умножения изображений
|
|
Определение свертки. Сверткой функций  и
и 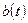 действительного переменного
действительного переменного 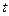 называется функция
называется функция  , определяемая равенством
, определяемая равенством
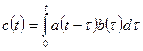 .
.
Символически свертку обозначают так: 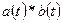 , то есть
, то есть
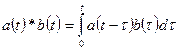 .
.
Операцию получения свертки функции будем называть свертыванием.
Пример 11. Пусть 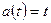 ,
,  тогда
тогда
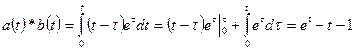 ,
,
то есть 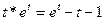 . (2.17)
. (2.17)
Пример 12. Пусть 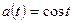 ,
, 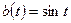 , тогда
, тогда
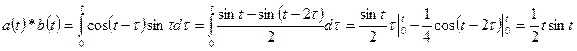 ,
,
то есть 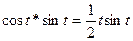 . (2.18)
. (2.18)
Понятие свертки имеет фундаментальное значение в современном построении операционного исчисления.
Теорема (умножения изображений). Произведение двух изображений 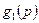 и
и  является изображением свертки соответствующих оригиналов.
является изображением свертки соответствующих оригиналов.
Доказательство.
Пусть 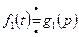 ,
, 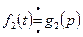 , тогда
, тогда
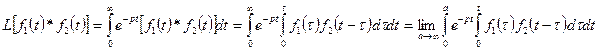 (2.19)
(2.19)
Изменяя порядок интегрирования в последнем интеграле, будем иметь:
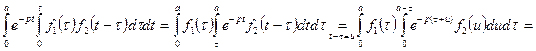
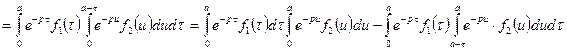 (2.20)
(2.20)
Обозначая последний интеграл 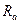 и учитывая, что существует
и учитывая, что существует  и
и 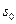 такие что
такие что 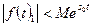 и
и 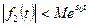 (в силу определения оригинала и предположения, что
(в силу определения оригинала и предположения, что 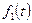 и
и 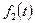 являются таковым), будем иметь
являются таковым), будем иметь
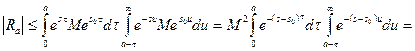
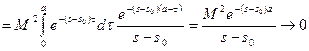 при
при 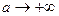 ,
, 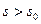 .
.
Следовательно, переходя к пределу при 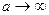 в равенстве (2.20), учитывая равенство (2.19) получим
в равенстве (2.20), учитывая равенство (2.19) получим
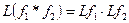
или 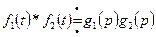 .
.
Пример 13. Найти оригинал 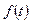 по изображению
по изображению 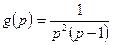 .
.
Так как 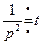 и
и 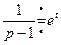 , то, применяя последовательно теорему умножения изображений и формулу (2.17), получим
, то, применяя последовательно теорему умножения изображений и формулу (2.17), получим 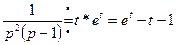 ,
,
то есть 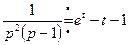 .
.
Пример 14. Найти оригинал 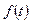 по изображению
по изображению 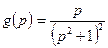 .
.
Так как 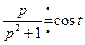 ,
, 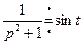 , то, применяя последовательно теорему умножения изображений и равенство (2.18) получим:
, то, применяя последовательно теорему умножения изображений и равенство (2.18) получим:
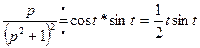 , т.е.
, т.е. 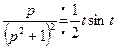 .
.
Дата публикования: 2014-11-02; Прочитано: 7107 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
