Явление электромагнитной индукции

Рассмотрим сущность электромагнитной индукции и принципы, которые приводят к этому явлению.

Предположим, что проводник 1-2 перемещается в магнитном поле со скоростью (рисунок 40). Тогда на заряды проводника действует сила Лоренца , направление которой определяется правилом правого винта. Под действием этой силы свободные заряды проводника перемещаются и возникает разделение зарядов (рисунок 40): положительный заряд накапливается на конце 2, отрицательный – на конце 1.

Разделение происходит до тех пор, пока электростатическая сила , направленная противоположно , не уравновесит последнюю .

На концах проводника возникает разность потенциалов. Устройство. В котором поде действием сторонних сил, направленных противоположно электростатическим, происходит разделение зарядов, называется источником ЭДС. Таким образом, движущийся в магнитном поле проводник является источником ЭДС. Возникновение ЭДС в проводнике, движущемся в магнитном поле, называется явлением электромагнитной индукции.

		b

Рисунок 40 Рисунок 41

Замкнем теперь проводник так, что система проводников образует контур (рисунок 41). Приложив к проводнику внешнюю силу 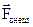будем перемещать контур а bсd вверх. В проводнике a b в соответствии со сказанным выше будет происходить разделение зарядов и возникнет ЭДС. В проводниках a dи bc, движущихся параллельно вектору разделение зарядов не происходит. Проводник cd с измерительным прибором находится в области, где 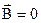, так что в нем разделение зарядов также не происходит. Следовательно, в контуре a bcd потечет ток, обусловленный возникшей на концах проводника a b ЭДС. Но на проводник с током, движущемся в магнитном поле, будет действовать магнитная cила (сила Ампера), направленная противоположно силе 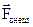. Непрерывное разделение зарядов в проводнике a b будет происходить при условии . Таким образом, для протекания тока в контуре a bcd необходимо, чтобы внешняя сила совершала работу , (53)

где dФ – изменение потока, пронизывающего контур , который образован геометрическим местом концов проводника при его движении (рисунок 42).

Подставляя в выражение (53) значение силы

тока . Получаем

. (54)

Рисунок 42

Из соотношения (54) находим ЭДС электромагнитной индукции

(55)

Можно показать, что формула (55) позволяет рассчитать ЭДС не только в контуре , образованным геометрическим местом концов проводника, но и в любом замкнутом контуре, если его пронизывает изменяющийся во времени магнитный поток.

Формула (55) выражает закон Фарадея, по имени выдающегося английского физика, который открыл явление электромагнитной индукции в 1831 году.

Закон (55) был открыт экспериментально в результате опытов, изучаемых в средней школе. Закон (55) читается так: ЭДС индукции в контуре равна скорости изменения магнитного потока, пронизывающего контур, взятой со знаком минус.

Знак «-«указывает направление индукционного тока согласно правилу, найденному петербургским профессором Э.Х. Ленцем.

Правило Ленца: индукционный ток во всех случаях направлен так, что его собственное магнитное поле противодействует изменению внешнего поля, или: его действие противоположно действию причины, вызвавшей ток.

Контур в магнитном поле как бы обладает инерционностью, то есть он стремится сохранить неизменным магнитный поток, который его пронизывает.

Рассмотрим действие этого правила на примере контура, который пронизывается изменяющимся магнитным потоком.

Пусть направление нормали к контуру , совпадает с вектором , тогда положительное направление обхода контура связано с правилом правого винта. Если индукция магнитного поля возрастает, то есть магнитный поток Ф возрастает, то по закону Ленца собственное магнитное поле направлено против внешнего поля ,то есть вниз, как показано на рисунке 43.

.

Следовательно, индукционный ток I_н, , вызвавший это поле, направлен по часовой стрелке. Действительно , противоположен положительному направлению обхода.

Рисунок 43