Намагниченность веществ

Различные вещества в магнитном поле намагничиваются, то есть приобретают магнитный момент и сами становятся источниками магнитных полей. Результирующее магнитное поле в среде является суммой полей, создаваемых проводниками с током и намагниченной средой, и поэтому отличается от магнитного поля в вакууме.

Вещества, способные намагничиваться, называются магнетиками.

Для объяснения намагничивания тел используем модель, предложенную Ампером. Согласно этой модели, в толще вещества имеются молекулярные замкнутые токи, которым соответствуют магнитные моменты (рисунок 25).

Рисунок 25 Рисунок 26

В отсутствие магнитного поля магнитные моменты ориентируются хаотически (рисунок 26), и в целом вещество не имеет магнитного момента. При помещении вещества в магнитное поле на магнитные моменты молекул действует вращающий момент , под действием которого они ориентируются вдоль силовых линий . Ориентирующему действию внешнего поля препятствует тепловое движение молекул, стремящееся разбросать магнитные моменты молекулярных токов по всем направлениям. В результате действия двух факторов – магнитного поля и теплового движения в магнетике устанавливается некоторая преимущественная ориентация магнитных моментов вдоль поля, что и обуславливает намагничивание магнетика (рисунок 27). Мерой намагниченности магнетика является вектор намагничивания

, (43)

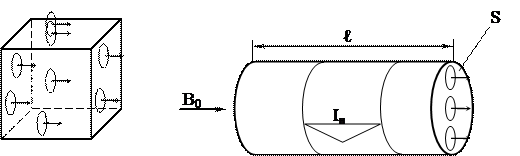Рисунок 27 Рисунок 28

Рассмотрим магнетик, помещенный в бесконечный соленоид, создающий однородное магнитное поле (рисунок 28). Намагничивание сердечника происходит вследствие ориентации магнитных моментов молекулярных токов. При этом в толще вещества молекулярные токи компенсируются, только на поверхности магнетика остается нескомпенсированным ток I_Н, который называется током намагничивания.

Магнитный момент образца равен

. (44)

С другой стороны, согласно определению (43)

, (45)

где V=S - объем магнетика.

Приравнивая выражения (44) и (45), получаем

, (46)

то есть величина вектора намагничивания равна току намагничивания, приходящемуся на единицу длины магнетика.

Вектор намагничивания является основной величиной, характеризующей магнитное состояние вещества. Экспериментально установлено, что вектор намагничивания пропорционален индукции внешнего магнитного поля

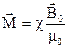, (47)

где c - магнитная восприимчивость, зависящая от природы магнетика, = 4p10^-7 Гн/м – магнитная постоянная. Намагничивание магнетиков приводит к возникновению в них собственного магнитного поля , которое накладываясь на внешнее магнитное поле , создает некоторое результирующее поле . (48)

Для нахождения внутреннего поля поместим магнетик в однородное Рисунок 29

магнитное поле (рисунок 29).

Вследствие взаимодействия внешнего поля с магнитными моментами атомов на поверхности магнетика возникнет ток намагничивания I_H. Индукцию на оси магнетика можно рассматривать как следствие протекания этого тока. С другой стороны магнетик можно рассматривать как бесконечно длинный соленоид, у которого индукция на оси равна произведению на суммарный ток его единицы длины. Ток намагничивания на единице длины магнетика численно равен вектору намагничивания М.Следовательно, можно записать 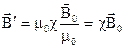(49)

В соответствии с формулами (47) и (49), находим индукцию результирующего поля

, (50)

где - магнитная проницаемость магнетика. По аналогии с электростатикой в теорию магнетизма вводится вспомогательный вектор , (51)

который называется напряженностью магнитного поля. Его величина зависит только от напряженности внешнего поля, напряженность характеризует индукцию, создаваемую внешним током (а не током намагничивания). С учетом (51) равенство (50) записывается в виде

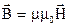. (52)

В скалярной форме . Сравним это выражение с формулой индукции на оси бесконечно длинного соленоида с магнетиком , где n - количество витков на единице длины соленоида. Из сравнения вытекает H = In. В СИ единицей напряженности является А/м.