Магнитное поле кругового тока

Рассчитаем индукцию магнитного поля, создаваемого круговым током, то есть током, протекающим по кольцу радиуса R (рисунок 12). Нахождение индукции в любой точке пространства представляет собой достаточно сложную задачу. На практике часто требуется рассчитать индукцию в любой точке А на оси ОХ, перпендикулярной площади контура с током и проходящей через его середину. Выделим на кольце два диаметрально противоположных элемента и 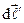такие, что . Согласно закону Био-Савара-Лапласа элемент 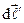создает в точке А индукцию такого направления, как это показано на чертеже. Аналогично элемент создает в этой точке индукцию 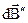, при этом ввиду симметрии 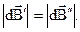Результирующая индукция от элементов 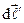и определяется векторной суммой

.

Из рисунка следует, что , (19)

где учтено, что .

Величина определяется из закона Био-Савара-Лапласа с учетом того, что угол между 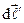и равен p/2: (20)

Подставляя формулу (20) в выражение (19), получаем

. (21)

Для того, чтобы найти индукцию в точке А от всего кольца. Необходимо проинтегрировать выражение (21) по длине полукольца

(22)

В частном случае при х = 0, из формулы (22) можно получить величину индукции в центре кольца (в точке О)

.

Из рисунка 12 видно, что направление вектора в любой точке А на оси ОХ определяется правилом правого винта: если головку винта вращать в направлении тока по часовой стрелке, то перемещение его острия укажет направление вектора .

Выражение (22) можно записать и в векторном виде. Для этого введем понятие магнитного момента контура

, (23)

где S – площадь контура,

- единичный вектор нормали к площади контура, направление которого связано с направлением тока правилом правого винта (рисунок 3).

Преобразуем выражение (5)

. (24)

Умножим левую и правую часть равенства (24) на вектор

,

Рисунок 13 а с учетом выражения (23)

. (25)

Формула (25) позволяет не только вычислить величину вектора на оси контура, но и определить его направление.