 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Циркуляция вектора магнитной индукции
|
|
По аналогии с электростатикой определяется понятие циркуляции вектора  по замкнутому контуру
по замкнутому контуру
 , где
, где 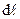 - элемент контура
- элемент контура  (рисунок 9).
(рисунок 9).
Вычислим циркуляцию вектора  для простейшего контура – окружности, в центре которой располагается бесконечно длинный проводник с током I. При этом полагаем, что направление обхода контура связано с направлением тока правилом правого винта (рисунок 10).
для простейшего контура – окружности, в центре которой располагается бесконечно длинный проводник с током I. При этом полагаем, что направление обхода контура связано с направлением тока правилом правого винта (рисунок 10).
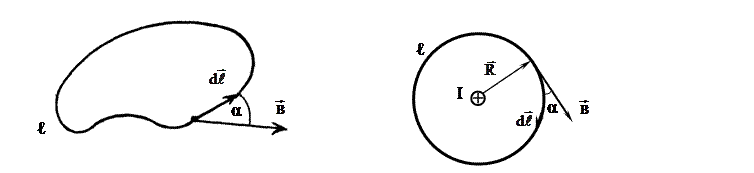
Рисунок 9 Рисунок 10
В соответствии с формулой (11) 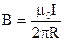 и
и 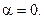 Тогда
Тогда
 (16)
(16)
Если же направление обхода контура сместить на противоположное, то a = p, cosa =-1 и интеграл  будет отрицательным. Это равнозначно тому, что ток при обходе такого контура был взят со знаком «минус». В рассмотренном примере контуром является окружность. Но оказывается, что выражение (16) справедливо для произвольного контура, охватывающего проводник с током. Более того, если произвольный контур охватывает несколько проводников произвольной формы с токами, то выражение для циркуляции вектора
будет отрицательным. Это равнозначно тому, что ток при обходе такого контура был взят со знаком «минус». В рассмотренном примере контуром является окружность. Но оказывается, что выражение (16) справедливо для произвольного контура, охватывающего проводник с током. Более того, если произвольный контур охватывает несколько проводников произвольной формы с токами, то выражение для циркуляции вектора  для такого контура аналогично выражению (16)
для такого контура аналогично выражению (16)
 , (17)
, (17)
где Ik берется со знаком «+», если его направление связано с направлением обхода контура правилом правого винта и со знаком «-«, если не связано.
Запись (17) является математическим выражением теоремы о циркуляции вектора  по замкнутому контуру: циркуляция вектора
по замкнутому контуру: циркуляция вектора  по замкнутому контуру, охватывающему проводники с токами равна алгебраической сумме токов, умноженной на постоянную
по замкнутому контуру, охватывающему проводники с токами равна алгебраической сумме токов, умноженной на постоянную  . Эта теорема широко применяется для расчета магнитных полей, создаваемых токами различной конфигурации.
. Эта теорема широко применяется для расчета магнитных полей, создаваемых токами различной конфигурации.
Из записи (17) следует, что в общем случае  , то есть в отличие от электростатического поля, для которого
, то есть в отличие от электростатического поля, для которого  , магнитное поле не является потенциальным.
, магнитное поле не является потенциальным.
Дата публикования: 2014-11-04; Прочитано: 793 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
