Поток вектора магнитной индукции

Поток вектора через произвольную поверхность dS определяется по аналогии с потоком вектора в электростатике. Выберем малую поверхность dS, в пределах которой поле вектора можно считать однородным (рисунок 7), тогда

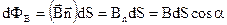, (12)

где n – единичный вектор нормали к поверхности.

Для неоднородного поля и поверхности произвольной формы поток вектора через такую поверхность находится интегрированием выражения (12)

(13)

Рисунок 7 Рисунок 8

Поток Ф_В численно равен количеству линий вектора , пересекающих эту поверхность. В СИ единицей потока является вебер (Вб), при этом 1 Вб = 1 Тл.м². Для замкнутых поверхностей вектор нормали направлен наружу (рисунок 8). На любой замкнутой S можно выделить две области, в которые линии вектора входят, и те, из которых они выходят. В первом случае и а во втором - и Тогда интеграл в правой части выражения (13) можно разбить на 2 интеграла . (14)

Ввиду непрерывности линий вектора количество их, входящих в поверхность , равно количеству, выходящих из , поэтому и

. (15)

Запись (15) отражает содержание теоремы Гаусса для магнитного поля: поток вектора магнитной индукции через замкнутую поверхность равен нулю. Смысл теоремы состоит в том, что в природе не существует неких магнитных зарядов, на которых обрывались бы линии вектора . Эти линии всегда замкнуты.