 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла
|
|
Пусть на отрезке  задана функция
задана функция 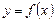 (рис. 10.1).
(рис. 10.1).
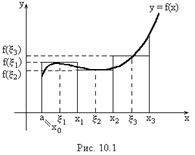
| Разобьем отрезок  на на 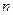 элементарных отрезков точками элементарных отрезков точками  , где , где 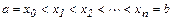 . На каждом отрезке разбиения выберем некоторую точку . На каждом отрезке разбиения выберем некоторую точку 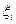 и положим и положим 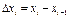 , где , где 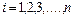 .
Сумму вида .
Сумму вида 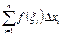 будем называть интегральной суммой для функции будем называть интегральной суммой для функции 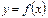 на отрезке на отрезке 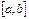 . .
|
Обозначим через  максимальную из длин отрезков
максимальную из длин отрезков  , т.е.
, т.е. 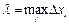 .
.
Определение. Определенным интегралом от функции 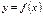 на отрезке
на отрезке  называется предел интегральной суммы при
называется предел интегральной суммы при 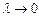 , т.е.
, т.е.
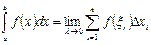 . (10.1)
. (10.1)
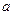 - нижний предел,
- нижний предел, 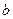 - верхний предел,
- верхний предел, 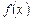 - подынтегральная функция,
- подынтегральная функция,  - подынтегральное выражение.
- подынтегральное выражение.
Замечание 1. Переменную под знаком интеграла можно обозначать любой буквой:  и т. д.
и т. д.
Замечание 2. В отличие от неопределенного интеграла 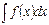 , который представляет семейство функций (первообразных), определенный интеграл
, который представляет семейство функций (первообразных), определенный интеграл 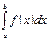 есть определенное число.
есть определенное число.
Дата публикования: 2014-11-04; Прочитано: 429 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
