 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры
|
|
Интегрирование - действие, обратное дифференцированию, то каждому правилу дифференцирования должно соответствовать некоторое правило интегрирования.
Пусть  и
и  - дифференцируемые функции от
- дифференцируемые функции от  х. Имеем:
х. Имеем:  , откуда
, откуда  .
.
Интегрируя обе части последнего равенства, получим:  , или
, или
 .
.
Это и есть формула интегрирования по частям.
Интегрирование по частям состоит в том, что подынтегральное выражение  представляется каким-либо образом в виде произведения двух множителей
представляется каким-либо образом в виде произведения двух множителей  и
и  (последний обязательно содержит
(последний обязательно содержит 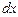 ) и согласно формуле данное интегрирование заменяется двумя:
) и согласно формуле данное интегрирование заменяется двумя:
1) при отыскании  из выражения для
из выражения для  ;
;
2) при отыскании интеграла от  .
.
Может оказаться, что эти два интегрирования легко осуществляются, тогда как заданный интеграл непосредственно найти трудно.
Правило интегрирования по частям нередко позволяет довести интегрирование до конца.
Пример. Найти  .
.
Решение. 
Пример. Найти  .
.
Решение. 
 .
.
Некоторые типы интегралов, берущиеся посредством формулы интегрирования по частям:
 , где , где  - многочлен - многочлен

| 
|
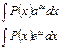
| 
|
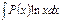
| 
|
Дата публикования: 2014-11-04; Прочитано: 532 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
