Свойства неопределенного интеграла

1) Производная от неопределенного интеграла равна подынтегральной функции, т.е. .

□ Доказательство. Дифференцируя левую и правую части равенства , получаем: .■

2) Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. .

□ Доказательство. По определению дифференциала и свойству 1 имеем: ■

3) Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. .

□ Доказательство. Рассматривая функцию как первообразную для некоторой функции , можно записать: и на основании дифференциал неопределенного интеграла , откуда .■

4) Постоянный множитель можно выносить за знак интеграла, т.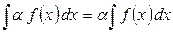е. , где - некоторое число.

5) Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. .