Свойства дифференциала аналогичны свойствам производной

1)	4)
2)	5)
3)

Инвариантность формы дифференциала

Если , то из (7.4) имеем .

Рассмотрим сложную функцию 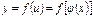, где .

Если функции и дифференцируемые функции от своих аргументов, то производная сложной функции равна .

Умножим обе части равенства на : . Таким образом, .

Это равенство означает, что формула дифференциала не изменится, если вместо функции от независимой переменной 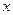рассматривать функцию от зависимой переменной 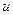. Это свойство дифференциала получило название инвариантности (т.е. неизменности) формы дифференциала.