Решение экстремальной задачи

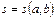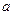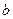Функция есть функция двух переменных и , а 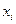, 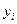- постоянные числа, найденные экспериментально.

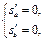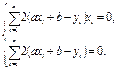Решаем систему уравнений или (8.2)

После алгебраических преобразований эта система принимает вид: (8.3)

Система (8.3) называется системой нормальных уравнений.

Пример. Результаты четырех измерений величин 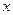и 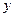приведены в таблице

х
у	0,2	0,3		1,2

Предполагая, что между переменным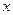и и 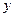существует линейная зависимость, найти эмпирическую формулу 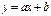методом наименьших квадратов.

Р ешение. Найдем необходимые для расчетов суммы:

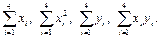
Вычисления оформим в виде вспомогательной таблицы.

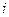
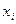
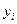
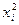
		0,2	0,2
		0,3	0,6
		1,2 1,2	4,8 4,8
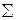
		2,7	8,6

Запишем систему нормальных уравнений (8.3):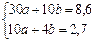

Ее решение 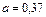, 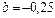дает исходную зависимость .

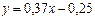33. Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала 1-го порядка.

Понятие о дифференциальных уравнениях. Общее и частное решения