 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод обратной матрицы
|
|
Запишем систему в матричной форме:
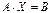, где
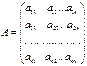- матрица коэффициентов при переменных,
- матрица-столбец переменных; 
- матрица столбец свободных членов.
Умножим слева обе части равенства на матрицу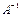 
:
;
;
;
.
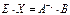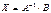Таким образом, решение системы в матричном виде 
.
Пример. Решить систему уравнений методом обратной матрицы. 
Р е ш е н и е: Обозначим 
; 
; 
.
Тогда в матричной форме система имеет вид: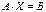 
. Определитель матрицы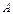 
, т.е. обратная матрица 
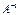существует: 
.
Определим 
,
Существенным недостатком решения систем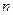 
линейных уравнений с 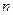переменными по формулам Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождения обратной матрицы.
Дата публикования: 2014-11-04; Прочитано: 346 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
