Решение системы линейных уравнений с неизвестными

Системы линейных уравнений находят широкое применение в экономике.

Система 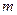линейных уравнений с 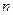переменными имеет вид:

,

где () - произвольные числа, называемые коэффициентами при переменных и свободными членами уравнений, соответственно.

Краткая запись: ().

Определение. Решением системы называется такая совокупность значений , при подстановке которых каждое уравнение системы обращается в верное равенство.

1) Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

2) Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

3) Две системы уравнений называются равносильными (эквивалентными), если они имеют одно и то же множество решений (например, одно решение).

Запишем систему в матричной форме:

Обозначим: , где

А – матрица коэффициентов при переменных, или матрица системы, Х – матрица-столбец переменных, В – матрица-столбец свободных членов.

Т.к. число столбцов матрицы 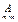равно числу строк матрицы , то их произведение:

Есть матрица-столбец. Элементами полученной матрицы являются левые части начальной системы. На основании определения равенства матриц начальную систему можно записать в виде: .

Теорема Крамера. Пусть - определитель матрицы 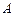системы, а - определитель матрицы, получаемой из матрицы 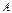заменой -го столбца столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам:

, - формула Крамера.