 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уравнение линии на плоскости
|
|
Определение. Уравнением линии (кривой) на плоскости 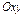 называется уравнение, которому удовлетворяют координаты
называется уравнение, которому удовлетворяют координаты  и
и 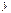 каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
 Если точка
Если точка 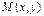 передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты
передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты 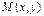 называются текущими координатами.
называются текущими координатами.
Любую линию в принципе можно выразить соответствующим уравнением. Однако не всякое уравнение на определяет на плоскости некоторую линию.
Например: 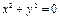 определяет только одну точку (0;0);
определяет только одну точку (0;0);
 не определяет никакого множества точек, т.к. левая часть уравнения не может равняться нулю.
не определяет никакого множества точек, т.к. левая часть уравнения не может равняться нулю.
Чтобы убедится, лежит ли точка 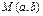 на данной линии
на данной линии 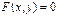 , надо проверить, удовлетворяют ли координаты этой точки уравнению
, надо проверить, удовлетворяют ли координаты этой точки уравнению 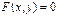 .
.
Уравнения линии могут быть самыми различными, однако надо отметить, что не каждое уравнение имеет геометрический образ в виде линии.
Взаимное расположение двух линий
Чтобы определить взаимное расположение 2-х линий, необходимо знать уравнений этих линий. Если система этих уравнений совместна, то линии имеют общие точки. В противном случае общих точек нет. Число общих точек равно числу решений системы уравнений
Например, прямая линия и окружность 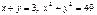 имеют 2 общие точки, так как система из этих уравнений имеет два решения:
имеют 2 общие точки, так как система из этих уравнений имеет два решения:
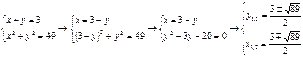 .
.
Дата публикования: 2014-11-04; Прочитано: 347 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
