 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Способ прямоугольных координат
|
|
На круговой кривой радиуса R кроме ее главных точек требуется фиксировать точки Р1, Р2, Р3 … (рис. 35) на равных расстояниях (5, 10, 15), выбираемых в зависимости от R и назначения кривой. Касательная тангенса РМ принимается за ось абсцисс с началом точке Р (HK), перпендикуляр к ней − за ось ординат, а прямоугольные координаты (x i, yi) точек P i вычисляются по формулам
х 1= R sinβ; х 2= R sin2β; х 3= R sin3β; (64)
y 1= R (1−cosβ); y 2= R (1−cos2β); y 3= R (1−cos3β);
где β = 
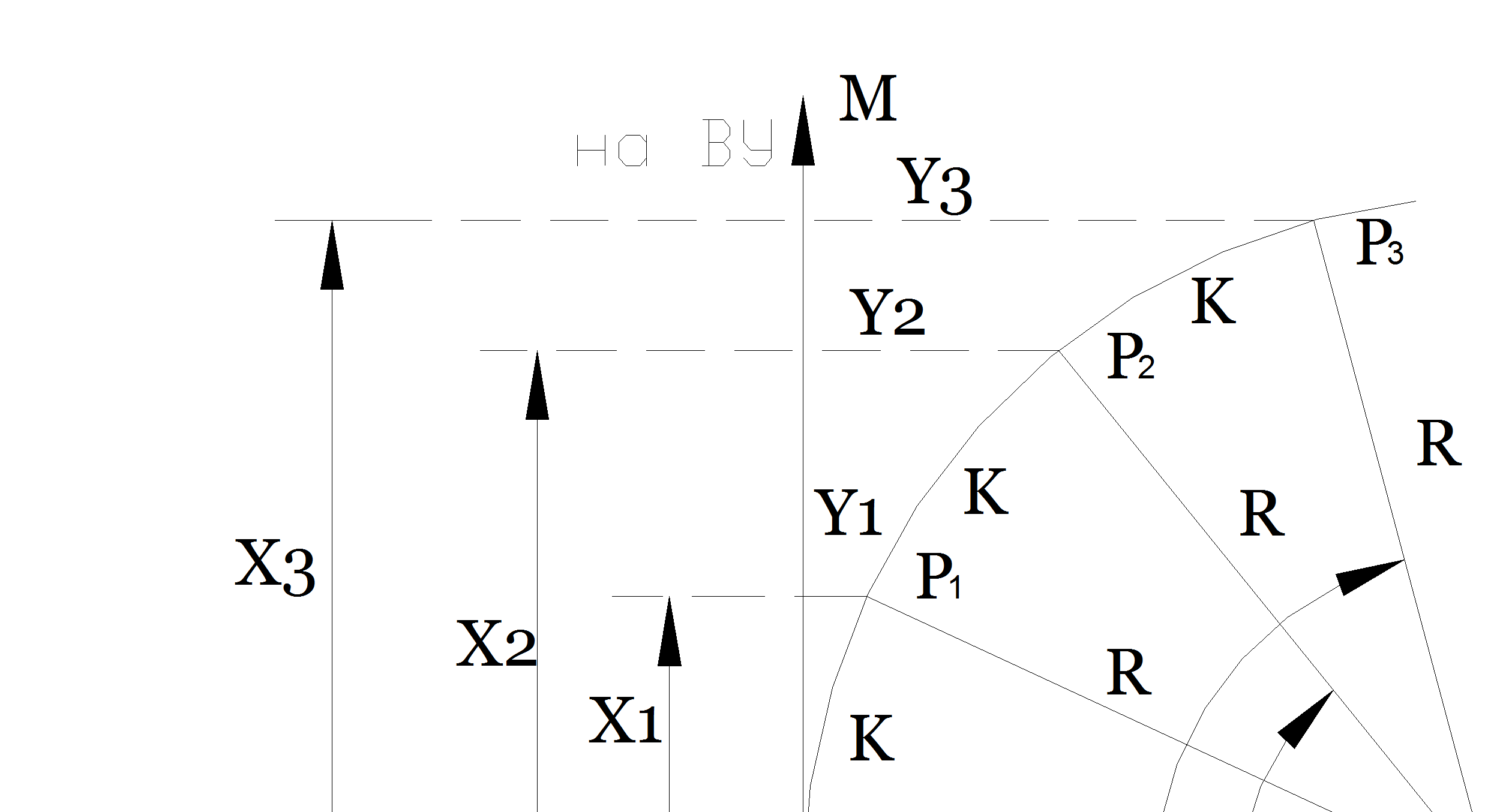 Рис. 33 Разбивка круговых кривых способом прямоугольных координат
Рис. 33 Разбивка круговых кривых способом прямоугольных координат
|
Для построения точек на местности надо из таблиц [4] по данным R и K выбрать координаты x i, y i.
Пример 2. R = 200 м; K = 5 м; Длина кривой K = 149,79 (из примера 1).
Из таблиц [2] (с. 225) выписываются значения координат. Построение точек на местности по этим координатам сводится к отложению лентой от точки Р по направлению касательной РМ значений х 1, х2 … хn, построению перпендикуляров и отложению от оснований их значений y1, y2…yn
| К | х | y | |
| 5,00 | 0,04 | ||
| 10,0 | 0,25 | ||
| 14,9 | 0,56 | ||
| … | |||
| 68,58 | 12,12 | ||
Разбивка ведется от начала и конца кривой к середине. Если в таблицах даются разности,,кривая без абсциссы", то для получения на касательной конца абсциссы надо отложить от точки Р на касательной отрезок l кп= l ко n, где n - порядковый номер точки, а l ко= К (шаг разбивки), отступить назад от конца этого отрезка на величину,,кривая без абсциссы" и в полученной точке построить перпендикуляр, отложив на нем x i.
Способ выгодно применять на открытой ровной местности.
Дата публикования: 2014-11-04; Прочитано: 2404 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
