Задача деления отрезка в данном отношении

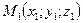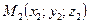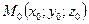Пусть даны две точки и . Требуется на прямой (рис.20) найти точку , которая разделила бы отрезок в заданном отношении 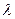, т.е. так, что . Согласно формуле (52)

,

.

Тогда по правилу (49) равенство примет вид , , .

Определяя 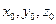из этих равенств, получим

, , , (53)

где , .

	z

			y

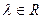Формулы (53) являются формулами деления отрезка в данном отношении. В частности, при получим формулы деления отрезка пополам:

, , . (54)

ПРИМЕР 17.1. Вершина треугольника 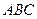имеет координаты . Найти длину медианы этого треугольника.

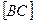Решение. Точка делит отрезок пополам. Тогда, согласно (53), получим

, , .

Искомое расстояние найдем по формуле (51):

.