Векторное произведение векторов

ОПРЕДЕЛЕНИЕ. Векторным произведением вектора на вектор 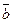называется вектор , удовлетворяющий условиям:

1) длина вектора численно равна площади параллелограмма, построенного на векторах и 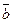, как на сторонах, т.е. ^ ;

2) вектор перпендикулярен обоим векторам и ;

3) вектор направлен в ту сторону, что если смотреть из его конца вдоль вектора, то кратчайший поворот вектора к вектору виден совершающимися против движения часовой стрелки. Векторное произведение вектора на вектор обозначается символом .

Введем декартовую систему координат и рассмотрим векторные произведения единичных векторов 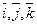. Покажем, что .

Действительно, если , то по определению векторного произведения:

1) ^ ;

2) ^ 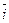, ^ 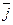. Но и ^ , ^ ;

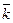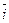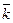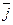3) если смотреть с конца вектора или 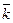, то кратчайший поворот вектора 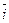к вектору 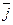виден происходящим против движения часовой стрелки (рис.23).

Итак, 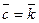. Следовательно, .

Аналогично доказывается, что

, , , ,

. , . (60)

Повторив вышеприведенные рассуждения для произвольных векторов и можно убедиться, что векторное произведение обладает свойствами:

1) ;

2) 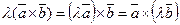для " ;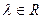

3) ;

4) , если или хотя бы один из векторов есть нулевой вектор;

5) .

Найдем выражение для векторного произведения векторов, заданных своими координатами. Пусть , . Тогда, согласно свойствам 2, 3, 4 и равенству (60), получим

Итак, если , , то

. (61)

ПРИМЕР 19.1. Сила приложена к точке . Определить момент силы относительно начала координат.

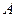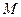Решение. Пусть точка некоторая точка . Моментом силы , приложенной к точке , относительно точки 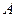называется вектор . По условию . Тогда, согласно формуле (61), получим

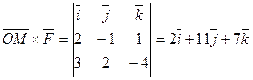. Ответ: .

ПРИМЕР 19.2. Даны вершины треугольника . Вычислить площадь этого треугольника.

Решение. Найдем векторы (рис.24). Имеем:

D

B

.

	A		C

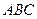Так как равен площади параллелограмма , то площадь треугольника найдется по формуле

Ответ: 14.

Из приведенных примеров следует, что векторное произведение в геометрии применяется при определении площадей многоугольников, в механике – при вычислении моментов.