Прямоугольная декартовая система координат

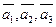Пусть в пространстве векторы образуют базис этого пространства. Выберем в произвольную точку 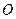и отложим с началом в этой точке базисные векторы. Совокупность точки 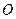и трех базисных векторов называется системой координат в пространстве . Ввиду произвольности выбора точки и выбора базисных векторов в можно построить бесконечное множество систем координат. Выберем за базисные векторы три взаимно перпендикулярных единичных вектора 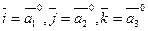. Совокупность точки 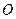и базисных векторов 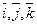называется прямоугольной декартовой системой координат в пространстве .

Выберем в произвольную точку 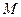и построим вектор 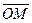. Так как векторы 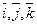образуют базис, то согласно (38) вектор 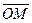можно разложить на компоненты по этому базису:

, (39)

где 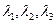- координаты вектора 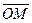в заданном базисе.

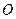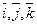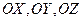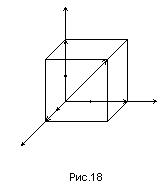
Проведем через точку в направлении векторов оси соответственно и спроектируем вектор 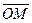на каждую из осей (рис.18).

Пусть точки 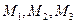есть проекция точки 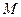на оси абсцисс, ординат и аппликат соответственно. Тогда

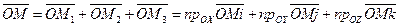. (40)

Из сравнения (40) с (39) следует, что координаты вектора 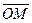определяются по формулам

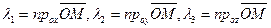. (41)

В прямоугольной декартовой системе эти координаты принято обозначать через 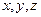соответственно и называть прямоугольными декартовыми координатами вектора 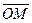или декартовыми координатами точки 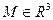. Итак,

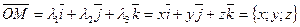. (42)

Координаты точки 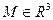записываются в форме 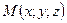. Пусть вектор 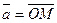задан в координатной форме 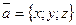. Так как этот вектор совпадает с диагональю прямоугольного параллелепипеда (рис.18), то его длина равна длине этой диагонали. Следовательно,

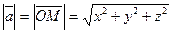. (43)

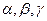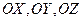Обозначим через углы между вектором и осями координат . Тогда из прямоугольных треугольников, 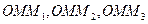получим

, ,

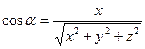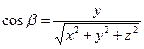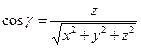. (44)

Косинусы углов 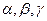, определяемые по (44), называются направляющими косинусами вектора . Нетрудно проверить, что направляющие косинуса связаны между собой соотношением

.

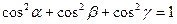ПРИМЕР 15.1. Доказать, что в прямоугольной декартовой системе координат векторы 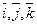имеют координаты .

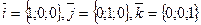Доказательство. Так как векторы 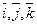образуют базис прямоугольной декартовой системе координат, то 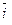^ 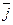, 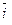^ 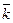, 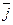^ 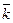, 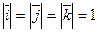. Следовательно,

.

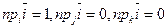Но .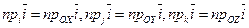

По формуле (38) получим, что

.

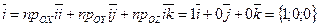Аналогично доказываются оставшиеся равенства.