 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Заданными в координатной форме
|
|
Пусть векторы 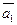 и
и 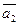 заданы в координатной форме:
заданы в координатной форме:
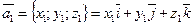 ,
,
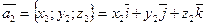 .
.
Непосредственно из теоремы 13.2 и 13.3 о проекциях векторов на ось и определения координат вектора (38) вытекают правила:
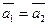 , если
, если 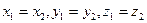 ; (46)
; (46)
 ; (47)
; (47)
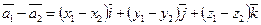 ; (48)
; (48)
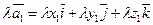 , где
, где 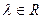 . (49)
. (49)
ПРИМЕР 16.1. (Условие коллинеарности двух векторов).
Установить условие коллинеарности векторов 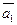 и
и 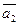 , если
, если 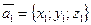 ,
, 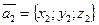 .
.
Решение. Так как векторы коллинеарны, то 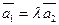 , где
, где 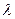 - некоторое число. Согласно (46)-(49) имеем
- некоторое число. Согласно (46)-(49) имеем
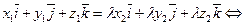
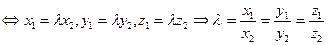 . (50)
. (50)
Легко проверяется, что если координаты векторов удовлетворяют равенствам (50), то 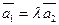 . Равенства (50) называются условием коллинеарности двух векторов.
. Равенства (50) называются условием коллинеарности двух векторов.
ПРИМЕР 16.2. (Координаты единичного вектора).
Определить координаты единичного вектора 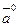 , если
, если 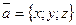 .
.
Решение. Согласно формуле (33) 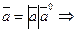
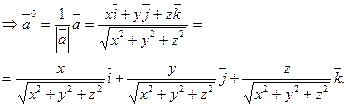
Из (44) следует, что
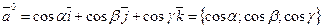 .
.
Дата публикования: 2014-11-04; Прочитано: 319 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
