Распределения, связанные с нормальным распределением

1. Распределение или распределение Пирсона (англ. статистик – 1857- 1936гг.)

Определение 1. Распределением с k степенями свободы называется распределение суммы квадратов k независимых случайных величин, распределенных по стандартному нормальному закону, так как

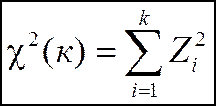, где

имеет нормальное распределение

Число k является параметром распределения. Число степеней свободы определяют как разность между числом суммируемых случайных величин и числом линейных связей, ограничивающих свободу изменения этих величин. Так как в сумме 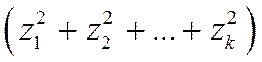слагаемые независимы, то число степеней свободы равно числу слагаемых, т.е. k.

Графики Пирсона при приведены на чертеже. Они показывают, что

- распределение асимметрично и обладает правосторонней асимметрией . При распределение случайной величины близко к стандартному нормальному закону

Определение 2. Дисперсия величины , т.е.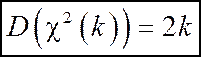

Определение 3. Если случайные величины и независимы, то их сумма имеет – распределение с числом степеней свободы 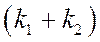, т.е.

2. Распределение Стьюдента (псевдоним англ. статиста В. Госсета) или

t- распределение.

Определение 4. Распределением Стьюдента называется распределение случайной величины Z:

, где

Z - случайная величина, распределенная по стандартному нормальному закону, т.е.

– независимая от Z случайная величина, имеющая - распределения с

k - степенями свободы.

Кривая 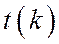- распределения с k степенями свободы симметрична оси ординат, но по сравнению с нормальной, более пологая. При t - распределение приближается к нормальному. При можно считать

t - распределение приближенно нормальным.

Определение 5. Математическое ожидание случайной величины, имеющей

t - распределение, в силу симметрии ее кривой распределения = 0, а ее дисперсия = , т.е.

3. Распределение Фишера (англ. статистик) или F- распределение.

Определение 6. Распределением Фишера называется распределение случайной величины:

, где

и - независимые случайные величины, имеющие 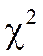- распределение соответственно с и степенями свободы.

Так как случайные величины и , то и .

При F - распределение приближается к нормальному закону.

§36 Закон больших чисел и предельные теоремы.

Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке акад. Колмогорова А.Н., совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату почти не зависящему от случая.