 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Дисперсия
|
|
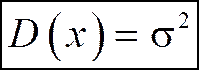
Определение 3. Дисперсия нормально распределенной случайной величины Х равна квадрату среднего квадратического отклонения.
Пример: Найти математическое ожидание и дисперсию случайной величины, распределенной по нормальному закону, если
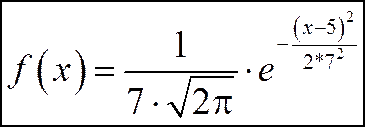
Ответ: M(x)=5, D(x)=49
График плотности нормального распределения имеет колоколообразную форму. Эта форма является отличительной чертой нормального распределения. Ее называют кривой Гаусса.
При изменении параметров а и 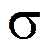 будет меняться нормальная кривая.
будет меняться нормальная кривая.
 f(x)
f(x)
Если 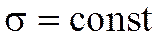 и
и 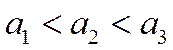 и меняется параметр а
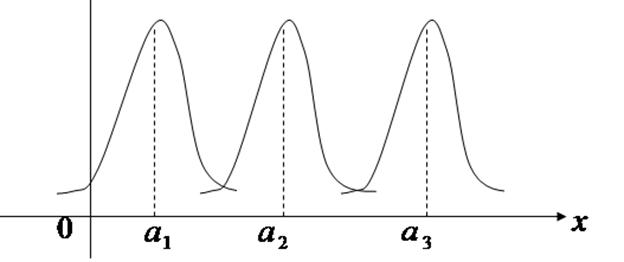
и меняется параметр а 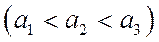 , т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы.
, т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы.
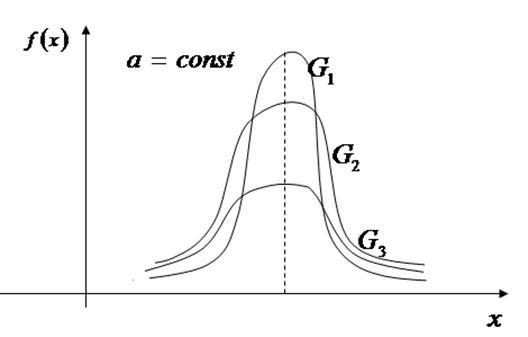
Если  и меняется параметр
и меняется параметр 
 , то меняется ордината максимума кривой
, то меняется ордината максимума кривой 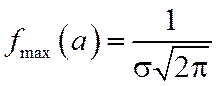 . При увеличении
. При увеличении 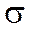 ордината максимума кривой уменьшается, но так как S под любой кривой должна оставаться = 1, то кривая становится более плоской, растягиваясь вдоль оси абсцисс; при уменьшении
ордината максимума кривой уменьшается, но так как S под любой кривой должна оставаться = 1, то кривая становится более плоской, растягиваясь вдоль оси абсцисс; при уменьшении  - нормальная кривая вытягивается вверх, одновременно сжимаясь с боков.
- нормальная кривая вытягивается вверх, одновременно сжимаясь с боков.
Таким образом, параметр 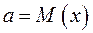 характеризует положение, а
характеризует положение, а 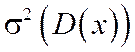 форму нормальной кривой.
форму нормальной кривой.
Определение 4. Нормальный закон распределения случайной величины с параметрами  и
и  , называется нормированным, а соответствующая нормальная кривая –нормированной.
, называется нормированным, а соответствующая нормальная кривая –нормированной.
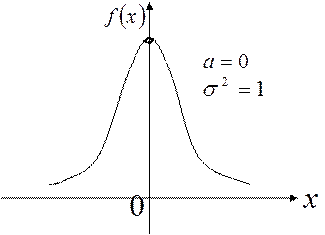

Дата публикования: 2014-11-04; Прочитано: 425 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
