Формула полной вероятности. Формула Байеса

Теорема. Если событие А может произойти только при условии появления одного из событий (гипотез) , образующих полную систему событий, то вероятность события А равна сумме произведений вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события А.

, где

Доказательство:

По условию события (гипотезы) 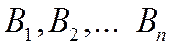образуют полную систему => они единственно возможные и несовместные. Т.к. гипотезы - единственно возможные, а событие А по условию теоремы может произойти только вместе с одной из гипотез, то

В силу того, что гипотезы несовместны, можно применить теорему сложения вероятностей:

.

По теореме умножения для зависимых событий , откуда получаем

, ч.т.д.

Пример: Известна сеть дорог между пунктами M и N.

N

Какова вероятность того, что путник дойдет из M в N?

А – путник дойдет.

В₁ – пошел по 1 дороге

В₂ - пошел по 2 дороге

В₃ – пошел по 3 дороге

В₄ – пошел по 4 дороге

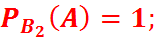
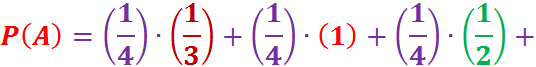
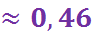
Пример: В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. К.в.т.,ч. извлеченный шар окажется белым, если равновероятны все возможные предположения о первоначальном составе шаров (по цвету).

Решение. А - извлечен белый шар

Гипотезы о первоначальном составе шаров:

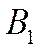- белых шаров нет;

- один белый шар;

- два белых шара.

Т.к. все гипотезы равновероятны и сумма их вероятностей = 1, то вероятность каждой из гипотез = 1/3, т.е.