Рекомендації щодо виконання

Більшість технічних систем і технологічних процесів описуються диференціальними рівняннями або системами диференціальних рівнянь високого порядку, аналітичний розв’язок яких досить ускладнений. У таких випадках для одержання розв’язку доцільним є застосування числових методів моделювання [7, 5, 8].

Усі відомі числові методи поділяються на дві групи: однокрокові та багатокрокові. Серед однокрокових найбільш поширені метод Ейлера, Гюна, метод рядів Тейлора, Рунге-Кутта, модифікований метод Ейлера-Коші. На практиці широкого застосування набули багатокрокові методи прогнозу-корекції, а саме метод Адамса-Бешфорса-Маултона, Мілна-Сімпсона та метод Хемінга.

Розглянемо особливості деяких методів та характерні для них рекурентні формули на прикладі розв’язання задачі на інтервалі з початковою умовою .

Найпростішим однокроковим методом є метод Ейлера, що полягає у розкладанні функції y (t) в області точки у ряд Тейлора. Для кожного значення t існує таке , що:

. (2.1)

Якщо і підставити до рівняння (2.1), то в результаті отримаємо вираз для :

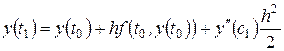. (2.2)

Якщо довжина кроку вибрана достатньо малою, то членом другого порядку () можна знехтувати й отримати вираз, що є наближенням Ейлера:

. (2.3)

Рекурентні співвідношення для наближеного розв’язання за допомогою методу Ейлера мають наступний вигляд:

, для . (2.4)

Розпочинаючи в точці розраховувати значення танґенса кута нахилу та рухатися по горизонталі на величину і по вертикалі на величину , а потім рухатися вздовж дотичної до y (t), можна дійти до точки і т.д. (рис. 2.1). Тобто геометрична інтерпретація методу Ейлера полягає в заміні інтеґральної кривої на кожному кроці інтеґрування відрізком прямої з одночасним знаходженням у кожній точці шуканої функції у числовій формі.

Рисунок 2.1 – Геометричне зображення методу Ейлера

Метод Ейлера має обмежене застосування у зв’язку зі значною похибкою, накопичуваною в процесі розрахунків.

Наступний підхід, метод Гюна, пропонує нову ідею побудови алгоритму наближеного розв’язання диференціальних рівнянь – на кожному кроці перше наближення знаходять методом Ейлера, а потім, щоб отримати остаточне значення, коректують його за формулою трапецій.

Для отримання розв’язку в точці функцію інтеґрують на інтервалі :

, (2.5)

де первісна функції є необхідною функцією y (t). Якщо розв’язати рівняння (2.5) відносно , то в результаті отримаємо:

. (2.6)

Для наближеного розрахунку інтеґрала в (2.6) використовують метод числового інтеґрування за допомогою формули трапецій з кроком :

. (2.7)

Використовуючи метод Ейлера, знаходять оцінку , що входить до правої частини. Якщо її підставити до (2.7), то для знаходження маємо:

. (2.8)

Рекурентні формули методу Гюна матимуть вигляд:

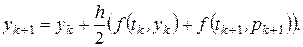(2.9)

Пояснимо геометричну інтерпретацію цього методу. Проведемо дотичну до кривої (рис. 2.2, а), що відповідає розв’язку у точці , і використаємо її, щоб знайти точку прогнозу . Розглянемо графік кривої (рис. 2.2, б), де в точках і значення функції і відповідно. Площа трапеції з вершинами і є наближенням до інтеґрала (2.6), що використовується для отримання остаточного значення в рівнянні (2.8).

а) б)

Рисунок 2.2 – Геометричне зображення методу Гюна:

а) прогноз похідної ;

б) корекція інтеґрала

Метод рядів Тейлора можна застосовувати в будь-якому випадку, бо він є еталоном, з яким порівнюють точність різних числових методів під час розв’язування задачі Коші. Цей метод призначений для отримання наближень з будь-яким ступенем точності.

Наближений числовий розв’язок задачі Коші на інтервалі за допомогою цього методу отримують, використовуючи на кожному підінтервалі розкладання функції y(t) у ряд Тейлора порядку N поблизу фіксованої точки . Загальна формула для методу Тейлора порядку N має вигляд:

, (2.10)

де для j =1, 2,..., N на кожному кроці k =0, 1, …, M.

Метод Рунге-Кутта 4-го порядку за точністю подібний до методу рядів Тейлора порядку N= 4. Метод ґрунтується на розрахунку 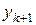за допомогою наступного рекурентного співвідношення:

(2.11)

де

(2.12)

Метод прогнозу-корекції Адамса-Бешфорса-Маултона (Adams-Bashforth-Moulton) – це багатокроковий метод, отриманий з фундаментальної теореми аналізу:

. (2.16)

Прогноз використовує наближення поліномом Лаґранжа для функції 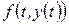, побудованою за точками . Це функція, що інтеґрується на інтервалі (рис. 2.3, а). Процес, що породжує прогноз Адамса-Бешфорса, має вигляд:

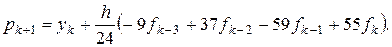(2.17)

Коректор можна отримати за аналогією. Наступний поліном Лаґранжа для функції 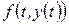будується за точками і новою точкою (рис. 2.3, б). Шляхом інтеґрування на відрізку отримуємо коректор Адамса-Маултона:

. (2.18)

а) б)

Рисунок 2.3 – Інтеґрування на інтервалі у методі Адамса-Бешфорса:

а) чотири вузли для прогнозу Адамса-Бешфорса

(використовують при екстраполяції);

б) чотири вузли для коректора Адамса-Маултона

(використовують при інтерполяції)

Інша найбільш поширена схема “прогноз-коректор” відома під назвою методу Мілна-Сімпсона. Прогноз методу ґрунтується на інтеґруванні функції 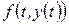на інтервалі :

. (2.19)

Прогноз використовує наближення поліномом Лаґранжа для 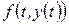, побудованим за точками і . Прогноз Мілна отримуємо після інтеґрування функції на інтервалі :

(2.20)

Коректор отримуємо за допомогою побудови полінома Лагранжа для функції 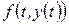за точками , і новою точкою , результатом інтеґрування якого на відрізку є відома формула Сімпсона:

(2.21)

Якщо для наближеного розв’язку використовують метод дискретної змінної, то існує два джерела похибки: дискретизація й округлення.

Припустимо, що – множина точок дискретного наближення, а – єдиний розв’язок. Тоді загальна похибка дискретизації дорівнює різниці між єдиним розв’язком і розв’язком, отриманим методом дискретної змінної:

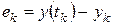для . (2.13)

Локальна похибка дискретизації є похибкою, зробленою в результаті одного кроку від до і визначається виразом:

для . (2.14)

Для вивчення поведінки похибки при різній довжині кроків використовують кінцеву загальну похибку , що є похибкою в кінці інтервалу, яка накопичена за M кроків:

. (2.15)

У табл. 2.1 наведено приклади програм для наближеного розв’язання диференціальних рівнянь за допомогою вище розглянутих однокрокових і багатокрокових числових методів, написаних мовою пакета Matlab.

Таблиця 2.1 – Програми для наближеного розв’язання диференціальних рівнянь за допомогою різних числових методів

Однокрокові методи
Метод Ейлера	Метод Гюна
function E=euler(a,b,ya,h) M=(b-a)/h; t=zeros(1,M+1); y=zeros(1,M+1); t=a:h:b; y(1)=ya; for j=1:M y(j+1)=y(j)+h*feval('f',t(j),y(j)); end E=[t'y']; function f=f(t,y) f=0.5*(t-y);	function H=heun(a,b,ya,h) M=(b-a)/h; t=zeros(1,M+1); y=zeros(1,M+1); t=a:h:b; y(1)=ya; for j=1:M k1=feval('f',t(j),y(j)); k2=feval('f',t(j+1),y(j)+h*k1); y(j+1)=y(j)+h*feval('f',t(j),y(j)); end H=[t'y']; function f=f(t,y) f=0.5*(t-y);
Метод рядів Тейлора 4-го порядку	Метод Рунге-Кутта 4-го порядку
function T4=taylor(a,b,ya,h) M=(b-a)/h; t=zeros(1,M+1); y=zeros(1,M+1); t=a:h:b; y(1)=ya; for j=1:M D=feval('df',t(j),y(j)); y(j+1)=y(j)+h*(D(1)+h*(D(2)/2+h* (D(3)/6+h*D(4)/24))); end T4=[t'y']; function df=df(t,y) df=[(t-y)/2 (2-t+y)/4 (-2+t-y)/8 (2-t+y)/16];	function R=rk4(a,b,ya,h) M=(b-a)/h; t=zeros(1,M+1); y=zeros(1,M+1); t=a:h:b; y(1)=ya; for j=1:M k1=h*feval(‘f’,t(j),y(j)); k2=h*feval(‘f’,t(j)+h/2,y(j)+k1/2); k3=h*feval(‘f’,t(j)+h/2,y(j)+k2/2); k4=h*feval(‘f’,t(j)+h,y(j)+k3); y(j+1)=y(j)+(k1+2*k2+2*k3+k4)/6; end R=[t'y']; function f=f(t,y) f=0.5*(t-y);

Продовження таблиці 2.1

Багатокрокові методи
Метод Адамса-Бешфорса-Маултона	Метод Мілна-Сімпсона
function A=abm(a,b,ya,h) M=(b-a)/h; t=zeros(1,M+1); y=zeros(1,M+1); t=a:h:b; n=length(t);   R=rk4(a,b,ya,h); for j=1:4 y(1,j)=R(j,2); end   if n<5,break,end; F=zeros(1,4);	function M=milne(a,b,ya,h) M=(b-a)/h; t=zeros(1,M+1); y=zeros(1,M+1); t=a:h:b; n=length(t);   R=rk4(a,b,ya,h); for j=1:4 y(1,j)=R(j,2); end   if n<5,break,end; F=zeros(1,4);
F=feval('f',t(1:4),y(1:4));   for k=4:n-1 p=y(k)+(h/24)*(F*[-9 37 -59 55]'); t(k+1)=t(1)+h*k; F=[F(2) F(3) F(4) feval('f',t(k+1),p)]; y(k+1)=y(k)+(h/24)*(F*[1 -5 19 9]'); F(4)=feval('f',t(k+1),y(k+1)); end A=[t'y']; function f=f(t,y) f=0.5*(t-y);	F=feval('f',t(1:4),y(1:4)); pold=0; yold=0; for k=4:n-1 pnew=y(k-3)+(4*h/3)*(F(2:4)*[2 -1 2]'); pmod=pnew+28*(yold-pold)/29; t(k+1)=t(1)+h*k; F=[F(2) F(3) F(4) feval('f',t(k+1),pmod)]; y(k+1)=y(k-1)+(h/3)*(F(2:4)*[1 4 1]'); pold=pnew; yold=y(k+1); F(4)=feval('f',t(k+1),y(k+1)); end M=[t'y']; function f=f(t,y) f=0.5*(t-y);
Метод Хемінга
function H=hamming(a,b,ya,h) M=(b-a)/h; t=zeros(1,M+1); y=zeros(1,M+1); t=a:h:b; n=length(t);   R=rk4(a,b,ya,h); for j=1:4 y(1,j)=R(j,2); end   if n<5,break,end; F=zeros(1,4); F=feval('f',t(1:4),y(1:4)); pold=0; cold=0;

Продовження таблиці 2.1

for k=4:n-1 pnew=y(k-3)+(4*h/3)*(F(2:4)*[2 -1 2]'); pmod=pnew+112*(cold-pold)/121; t(k+1)=t(1)+h*k; F=[F(2) F(3) F(4) feval('f',t(k+1),pmod)]; cnew=(9*y(k)-y(k-2)+3*h*(F(2:4)*[-1 2 1]'))/8; y(k+1)=cnew+9*(pnew-cnew)/121; pold=pnew; cold=cnew; F(4)=feval('f',t(k+1),y(k+1)); end H=[t'y']; function f=f(t,y) f=0.5*(t-y);