Неприводимые многочлены над полями комплексных и вещественных чисел

Следующие пять многочленов демонстрируют некоторые элементарные свойства неприводимых многочленов:

,

,

,

,

.

Над кольцом 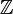целых чисел, первые два многочлена — приводимые, последние два — неприводимые. (Третий вообще не является многочленом над целыми числами).

Над полем рациональных чисел, первые три многочлена являются приводимыми, двое других — неприводимыми.

Над полем 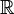действительных чисел, первые четыре многочлена — приводимые, но является неприводимым. В поле действительных чисел неприводимыми являются линейные многочлены и квадратичные многочлены без действительных корней. Например разложение многочлена в поле действительных чисел имеет вид . Оба множителя в данном разложении являются неприводимыми многочленами.

Над полем комплексных чисел, все пять многочленов — приводимые. Фактически, каждый отличный от константы многочлен над может быть разложен на множители вида:

где 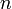— степень многочлена, 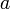— старший коэффициент, 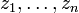— корни . Поэтому единственными неприводимыми многочленами над являются линейные многочлены (основная теорема алгебры).

Конечные поля

Многочлены с целочисленными коэффициентами, которые являются неприводимыми над полем могут быть приводимыми над конечным полем. Например, многочлен является неприводимым над , но над полем из двух элементов мы имеем: