 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Деление с остатком
|
|
Определение. Пусть 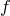 и
и 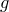 — многочлены,
— многочлены, 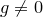 . Будем говорить, что
. Будем говорить, что 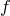 поделен на
поделен на 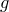 с остатком, если
с остатком, если 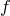 представлен в виде
представлен в виде 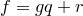 , где
, где 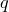 и
и  — многочлены, причем
— многочлены, причем 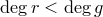 .
.
Полином  называется остатком от деления
называется остатком от деления 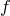 на
на 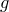 ,
, 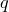 — неполным частным.
— неполным частным.
Пример. 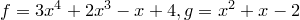 .
.
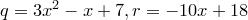 .
.
Теорема. (о делении с остатком). Пусть 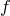 и
и 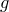 — полиномы над полем
— полиномы над полем  ,
, 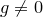 . Тогда существуют единственные многочлены
. Тогда существуют единственные многочлены 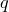 и
и  над полем
над полем  такие, что
такие, что 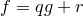 и
и 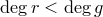 .
.
Доказательство. Существование.
Пусть 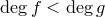 . Положим
. Положим 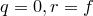 .
.
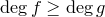 .
.
Предположим, что теорема верна не для любого полинома 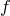 (
(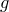 фиксируем). Среди всех многочленов
фиксируем). Среди всех многочленов 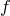 , для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его
, для которых теорема неверна, выберем многочлен наименьшей степени и обозначим его 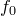 :
:
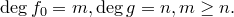
Пусть 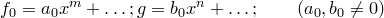 . Положим
. Положим
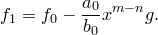
Коэффициент при 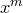 в многочлене
в многочлене  равен
равен 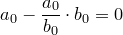 . Следовательно,
. Следовательно, 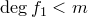 . Значит, для многочлена
. Значит, для многочлена  теорема верна. Существуют такие
теорема верна. Существуют такие 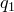 и
и  , что
, что 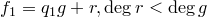 . Тогда
. Тогда

Получили противоречие с тем предположением, что есть многочлены, для которых теорема неверна.
Единственность. Предположим, что
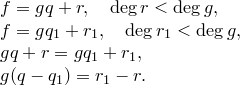
1) 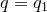 . Значит,
. Значит, 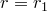 ,
,
2) 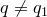 .
.
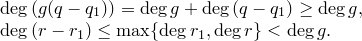
Получили противоречие. Этот случай невозможен.
Теорема Безу
Теорема. Остаток от деления многочлена 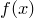 на многочлен
на многочлен  равен
равен 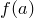 .
.
Доказательство. Степень остатка меньше 1, следовательно, остаток — константа. Пусть  — остаток.
— остаток.
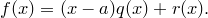
Это равенство верно при любых значениях 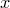 . Положим
. Положим  :
:

Дата публикования: 2015-11-01; Прочитано: 718 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
