 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Нормальная форма записи многочленов. Степень многочлена и ее свойства. Кольцо многочленов над областью целостности
|
|
Фробениусовой нормальной формой линейного оператора называется блочно-диагональная матрица, состоящая из фробениусовых клеток вида.
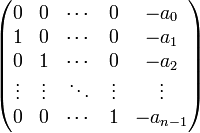
и является матрицей данного линейного оператора в некотором базисе.
Свойства
- Коэффициентами характеристического многочлена фробениусовой клетки являются
 ,
, 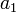 ,
,  ,
, 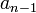 из приведённой выше матрицы, и многочлен имеет вид
из приведённой выше матрицы, и многочлен имеет вид 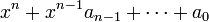 .
.
Свойства
- Кольцо многочленов
 факториально: любой многочлен разлагается в произведение неприводимых многочленов, причем это разложение определено однозначно с точностью до постоянных множителей.
факториально: любой многочлен разлагается в произведение неприводимых многочленов, причем это разложение определено однозначно с точностью до постоянных множителей. - Над полем вещественных чисел любой неприводимый многочлен одной переменной имеет степень 1 или 2, причем многочлен 2-й степени неприводим тогда и только тогда, когда он имеет отрицательный дискриминант.
- Над любым полем алгебраических чисел существуют неприводимый многочлен сколь угодно высокой степени; например, многочлен
 , где
, где  и
и  ― некоторое простое число, неприводим в силу критерия Эйзенштейна.
― некоторое простое число, неприводим в силу критерия Эйзенштейна. - Если
 — конечное поле из
— конечное поле из 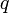 элементов, а
элементов, а 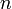 — натуральное число, то существует хотя бы один неприводимый многочлен степени n из
— натуральное число, то существует хотя бы один неприводимый многочлен степени n из  .
. - Предположим
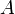 ― целозамкнутое кольцо с полем частных
― целозамкнутое кольцо с полем частных  (например
(например  и
и  ) и
) и  ― многочлен одной переменной со старшим коэффициентом 1, тогда
― многочлен одной переменной со старшим коэффициентом 1, тогда  в
в  , причем
, причем 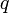 и
и  имеют старший коэффициент 1, то
имеют старший коэффициент 1, то  .
. - Редукционный критерий неприводимости. Пусть задан гомоморфизм областей целостности
 . Если степень многочлена
. Если степень многочлена  совпадает со степенью многочлена
совпадает со степенью многочлена  и
и  неприводим над полем частных области
неприводим над полем частных области  , то не существует разложения
, то не существует разложения  , где
, где  и отличны от константы.
и отличны от константы. - Например, многочлен
 со старшим коэффициентом
со старшим коэффициентом  прост в
прост в  (и, следовательно, неприводим в
(и, следовательно, неприводим в  ), если прост многочлен
), если прост многочлен  , полученный из
, полученный из  редукцией коэффициентов по модулю простого числа.
редукцией коэффициентов по модулю простого числа.
Область целостности (или целостное кольцо, или область цельности или просто область) — понятие абстрактной алгебры: ассоциативное коммутативное кольцо без делителя нуля (произведение ненулевых элементов не равно 0).
Эквивалентное определение: область целостности — это ассоциативное коммутативное кольцо, в котором нулевой идеал {0} является простым. Любая область целостности является подкольцом своего поля частных.
Примеры
- Простейший пример области целостности — кольцо целых чисел
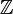 .
. - Любое поле является областью целостности. С другой стороны, любая артинова область целостности есть поле. В частности, все конечные области целостности суть конечные поля.
- Кольцо многочленов с коэффициентами из некоторого целостного кольца также является целостным. Например, целостными будут кольцо
 многочленов одной переменной с целочисленными коэффициентами и кольцо
многочленов одной переменной с целочисленными коэффициентами и кольцо  многочленов двух переменных с вещественными коэффициентами.
многочленов двух переменных с вещественными коэффициентами. - Множество действительных чисел вида
 есть подкольцо поля
есть подкольцо поля 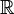 , а значит, и область целостности. То же самое можно сказать про множество комплексных чисел вида
, а значит, и область целостности. То же самое можно сказать про множество комплексных чисел вида  , где
, где 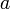 и
и  целые (множество Гауссовых целых).
целые (множество Гауссовых целых). - Пусть
 — связное открытое подмножество комплексной плоскости
— связное открытое подмножество комплексной плоскости  . Тогда кольцо
. Тогда кольцо  всех голоморфных функций
всех голоморфных функций 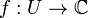 будет целостным. То же самое верно для любого кольца аналитических функций, определённых на связном подмножестве аналитического многообразия.
будет целостным. То же самое верно для любого кольца аналитических функций, определённых на связном подмножестве аналитического многообразия. - Если
 — коммутативное кольцо, а
— коммутативное кольцо, а  — идеал в
— идеал в  , то факторкольцо
, то факторкольцо  целостное тогда и только тогда, когда
целостное тогда и только тогда, когда  — простой идеал.
— простой идеал.
Дата публикования: 2015-11-01; Прочитано: 2008 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
