 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Взаимно простые многочлены. Определение, свойства
|
|
Т. Критерий взаимной простоты.
Для того, чтобы многочлены f(x) и g(x) из F[x] были взаимно простыми, необходимо и достаточно, чтобы в F[x] существовали такие u(x) и v(x), что u(x)f(x)+v(x)g(x)=1.
Док-во:
- Необходимость: очевидно.
- Достаточность: Пусть d(x) - НОД многочленов f(x) и g(x). Значит каждое из слагаемых левой части делится на d(x). А значит и правая часть делится на d(x). Следовательно d(x) - ненулевая константа.
Свойства взаимно простых многочленов.
Т. Если многочлен f(x) взаимно прост с каждым из многочленов g(x) и h(x), то он взаимно прост и с их произведением.
Док-во:
Из условия следует, что найдутся такие u(x), v(x), u1(x), v1(x), что:
u(x)f(x)+v(x)g(x)=1
u1(x)f(x)+v1(x)h(x)=1.
Складывая эти неравенства, получим:
(u(x)u1(x)f(x)+u(x)v1(x)h(x)+v(x)g(x)u1(x))*f(x) + (v(x)v1(x))*g(x)h(x) = 1
Т. f(x)h(x):g(x), НОД(f(x),g(x))=1 ===> h(x):g(x).
Док-во:
u(x)f(x)+v(x)g(x)=1
u(x)f(x)h(x)+v(x)g(x)h(x)=h(x)
1-ое слагаемое делится на g(x) по условию, второе - очевидно. След-но правая часть делится на g(x).
Т. f(x):g(x), f(x):h(x), НОД(g,h)=1, ===> f(x):g(x)h(x).
Док-во:
Сущ. q(x) такое, что f(x)=q(x)g(x) ===> q(x):h(x).
Сущ. q1(x) такое, что q(x)=q1(x)h(x) ===> f(x)=q1(x)g(x)h(x).
28. Неприводимые многочлены. Определение, свойства.
Неприводимый многочлен — многочлен, неразложимый на нетривиальные (неконстантные) многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов.
Определение
Неприводимый многочлен над полем  ― многочлен
― многочлен  от
от 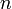 переменных над полем
переменных над полем  является простым элементом кольца
является простым элементом кольца  , то есть, непредставим в виде произведения
, то есть, непредставим в виде произведения  , где
, где 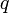 и
и  ― многочлены с коэффициентами из
― многочлены с коэффициентами из  , отличные от констант.
, отличные от констант.
Многочлен называется абсолютно неприводимым, если он неприводим над алгебраическим замыканием поля коэффициентов. Абсолютно неприводимые многочлены одной переменной ― это многочлены 1-й степени и только они. В случае нескольких переменных существуют абсолютно неприводимые многочлены сколь угодно высокой степени — например, любой многочлен вида

абсолютно неприводим.
Свойства
- Кольцо многочленов
 факториально: любой многочлен разлагается в произведение неприводимых многочленов, причем это разложение определено однозначно с точностью до постоянных множителей.
факториально: любой многочлен разлагается в произведение неприводимых многочленов, причем это разложение определено однозначно с точностью до постоянных множителей. - Над полем вещественных чисел любой неприводимый многочлен одной переменной имеет степень 1 или 2, причем многочлен 2-й степени неприводим тогда и только тогда, когда он имеет отрицательный дискриминант.
- Над любым полем алгебраических чисел существуют неприводимый многочлен сколь угодно высокой степени; например, многочлен
 , где
, где  и
и  ― некоторое простое число, неприводим в силу критерия Эйзенштейна.
― некоторое простое число, неприводим в силу критерия Эйзенштейна. - Если
 — конечное поле из
— конечное поле из 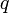 элементов, а
элементов, а 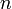 — натуральное число, то существует хотя бы один неприводимый многочлен степени n из
— натуральное число, то существует хотя бы один неприводимый многочлен степени n из  .
. - Предположим
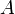 ― целозамкнутое кольцо с полем частных
― целозамкнутое кольцо с полем частных  (например
(например  и
и  ) и
) и  ― многочлен одной переменной со старшим коэффициентом 1, тогда
― многочлен одной переменной со старшим коэффициентом 1, тогда  в
в  , причем
, причем 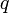 и
и  имеют старший коэффициент 1, то
имеют старший коэффициент 1, то  .
. - Редукционный критерий неприводимости. Пусть задан гомоморфизм областей целостности
 . Если степень многочлена
. Если степень многочлена  совпадает со степенью многочлена
совпадает со степенью многочлена  и
и  неприводим над полем частных области
неприводим над полем частных области  , то не существует разложения
, то не существует разложения  , где
, где  и отличны от константы.
и отличны от константы.
Например, многочлен  со старшим коэффициентом
со старшим коэффициентом  прост в
прост в  (и, следовательно, неприводим в
(и, следовательно, неприводим в  ), если прост многочлен
), если прост многочлен  , полученный из
, полученный из  редукцией коэффициентов по модулю простого числа.
редукцией коэффициентов по модулю простого числа.
29. Каноническое разложение многочлена на неприводимые многочлены.
Рассмотрим самый общий случай. Пусть дано некоторое поле многочленов GF (q), где q = pn, n — степень модуля q, а p — характеристика. Обозначим через g 1(x), g 2(x),..., gq –1(x) различные неприводимые многочлены над полем чисел GF (p), отвечающие примитивным корням: c 1, c 2,..., cq –1. Утверждается, что существует единственно возможное разложение многочлена xq –1 – 1 на множители gi (x); или, что одно и то же, каждый элемент ci является корнем многочлена xq –1 – 1; или, наконец, исходный приводимый многочлен можно представить в виде произведения порождающего g (x) и проверочного h (x) многочленов:

Здесь c — примитивный корень порождающего многочлена g (x), а для проверочного многочлена h (x) берутся те степени c j, которые не вошли в многочлен g (x). Как видим, действия с многочленами во многом схожи с действиями над числами. Приводимый многочлен вида xq –1 – 1 играет роль составного числа a, его примитивные корни c 1, c 2,..., cq –1 ассоциируются с простыми сомножителями p 1, p 2,..., p k, а последняя формула разложения на множители аналогична каноническому разложению составного числа a = p 1 n 1 p 2 n 2.... pknk. Многочлены g (x) и h (x) играют роль двух делителей числа a = g · h. Корни исходного многочлена играют роль базиса, по которому многочлены g (x) и h (x) могут быть разложены. Таким образом, теория полей многочленов смыкается с теорией линейных пространств. Покажем, как это осуществляется практически.
Если c — примитивный корень многочлена g (x), то
g (c) = g 0 + g 1 c + g 2 c 2 +... + gncn = 0.
Выразим степени корней cn и cn +1 через линейную комбинацию младших степеней корней c, c 2,..., cn –1 (gn = 1):
cn = g 0 + g 1 c + g 2 c 2 +... + gn –1 cn –1,
cn +1 = g 0 c + g 1 c 2 + g 2 c 3 +...
... + gn –1(g 0 + g 1 c + g 2 c 2 +... + gn –1 cn –1).
Следовательно, все степени ci при i > n линейно выражаются через первые n степеней; число таких комбинаций не превышает величину q – 1. Следует также иметь в виду, что не только g (c) = 0, но и
g (c 2) = g (c 3) =... = g (cq –1) = 0.
Дата публикования: 2015-11-01; Прочитано: 10190 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
