Алгоритм Евклида для целых чисел

Пусть 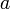и — целые числа, не равные одновременно нулю, и последовательность чисел

определена тем, что каждое — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

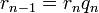
Тогда НОД(a, b), наибольший общий делитель 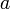и , равен , последнему ненулевому члену этой последовательности.

Существование таких 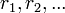, то есть возможность деления с остатком на 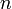для любого целого и целого , доказывается индукцией по m.

Корректность этого алгоритма вытекает из следующих двух утверждений:

• Пусть , тогда НОД (a, b) = НОД (b, r).
• НОД(0, ) = для любого ненулевого (т.к. 0 делится на любое целое число, кроме нуля).

Проще сформулировать алгоритм Евклида так: если даны натуральные числа 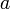и и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.

Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена^[1], а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида . Метод назван в честь Уильяма Джорджа Горнера (англ.).