Сдвиг и кручение

§ 6. Понятие о сдвиге (срезе)

Под сдвигом понимается угловая деформация, которая численно равна измене­нию величины первоначально прямого угла в радианах и обозначается γ.

Для демонстрации явления сдвига рассмотрим элементарный прямоугольник АBDС,рис.7.

После деформации прямоугольник АBDСпревращается в параллелограмм АBD^/С^/ Величина СС^/= а, на которую сечение СD сдвинулось относительно соседнего сечения АВ, называется абсолютным сдвигом.

Угол γ, на который изменился прямой угол параллелепипеда, назы­вается относительным сдвигом и яв­ляется мерой сдвига. В области упругих деформаций этот угол очень мал и может быть определен как:

Здесь в силу малости угла тангенс его можно заменять самим углом. Из формулы видно, что относительный сдвиг - есть отношение абсолютного сдвига к расстоянию между рассматриваемыми сдвигаемыми сечениями.

Для определения внутренних сил в сечении стержня, между двумя срезываю­щими силами Р применим метод сечений. Для этого отбросим одну часть тела от­носительно интересующего нас сечения, а действие отброшенной части на остав­шуюся заменим внутренними силами, рис.8.

Согласно рис. 8б внутренние силы должны вызывать касательные напряжения, ко­торые при условии равномерного их распределения по сечению можно определить:

, (6.1)

где F - площадь поперечного сечения;

Р - сдвигающая (срезывающая) сила.

Экспериментально подтвержден для случая сдвига закон Гука:

где - коэффициент пропорциональности, зависящий от природы материала.

Зная, что и можем перейти к следующему виду закона Гука:

, (6.2)

где G – есть модуль сдвига или модуль упругости второго рода.

Модуль сдвига обычно составляет некоторую часть от модуля нормальной упругости Е:

, (6.3)

аточная зависимость между упругими постоянными:

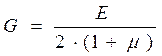, (6.4)

гдеμ - коэффициент Пуассона.

Модуль сдвига для стали кг/см².

Расчетное уравнение при сдвиге:

, (6.5)

где - допускаемое касательное напряжение.

Чистым сдвигом называется такой случай плоского напряженного состояния, при котором по двум взаимно-перпендикулярным площадкам действуют лишь касательные напряжения, а нормальные напряжения равны нулю.

Кручение

Под кручением понимают такой вид деформации, когда в поперечных сечениях бруса возникают крутящие моменты.

Результаты опытов над кручением круглого бруса позволили принять следуют допущения при изучении теории кручения:

1) плоские поперечные сечения круглого бруса остаются плоскими и после деформации (гипотеза плоских сечений);

2) радиусы, проведенные в поперечных сечениях, после деформации сохраняют свою длину;

3) углы поворота сечения тем больше, чем дальше сечение отстоит от мест закрепления;

4) образующие стержня превращаются в винтовые линии, т.е. происходит сдвиг частиц, и в поперечных сечениях возникают касательные напряжения;

5) принимается закон Гука, т.е. соблюдается пропорциональность между крутящим моментом и углом закручивания в пределах упругих деформаций.

Для определения касательных напряжений применим метод сечений. Мысленно вырежем из круглого бруса элемент радиусом rи длиной dz (рис.9а), из которого в свою очередь, вырежем другой элемент произвольного радиуса ρ(рис. 9б).

Положим, что разность полных сдвигов двух сечений на бесконечно малом расстоянии dz будет nn₁, тогда относительный сдвиг ;

Если обозначить весьма малую разность полных углов закручивания на длине dz через dφ можно написать .

Тогда выражение для относительного сдвига представится в виде:

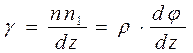
Используем закон Гука при сдвиге . Подставив в эту формулу

выражение для относительного сдвига, получим пока еще не окончательную формулу касательного напряжения в произвольной точке рассматриваемого сечения:

, (7.1)

где ρ - расстояние от этой точки до оси бруса.

Величина элементарной внутренней касательной силы в произвольной точке се­чения равна 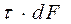; момент этой силы, действующей по площадке dFотно­сительно оси бруса

Полный момент внутренних касательных сил относительно оси бруса будет равен:

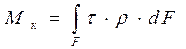, (7.2)

а так как , то можно написать

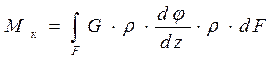
или (7.3)

Но интеграл представляет собой полярный момент инерции площади сечения, поэтому

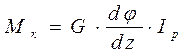, (7.4)

откуда , (7.5)

где dφ - элементарный угол закручивания на длине dz.

Полный угол закручивания:

или окончательно (7.6)

Произведение называют жесткостью сечения бруса при кручении.

Из полученной формулы (7.6) следует, что величина угла закручивания φ прямо пропорциональна крутящему моменту М_к и длине бруса l и обратно про­порциональна жесткости сечения при кручении .

Величина угла закручивания φ измеряется в радианах. Чтобы подучить φ в градусах, необходимо применять формулу:

(7.7)

Подставляя в выражение (7.1) значение (7.5), получим формулу для опреде­ления касательных напряжений:

,

окончательно - (7.8)

В формуле (7.8) величина постоянная для рассматриваемого се­чения, следовательно, касательные напряжения изменяются прямопропорционально расстоянию ρ.

Наибольшее значение величины касательных напряжений будет в крайних точ­ках сечения бруса, т.е. при

(7.9)

Величина называется полярным моментом сопротивления сечения бруса.