Доказательство логической непротиворечивости геометрии Лобачевского

1. В этом параграфе мы докажем непротиворечивость системы аксиом планиметрии Лобачевского, состоящей из четырех групп I_1-3, II_1-4, III_1-5, IV_1-2 аксиом Гиль­берта (аксиомы абсолютной планиметрии) и аксиомы V* Лобачевского. При решении этой задачи предполагается, что евклидова геометрия (т. е. система аксиом _H Гиль­берта) непротиворечива. Мы построим из объектов евклидовой плоскости модель плоскости Лобачевского, которая называется евклидовой моделью Кэли — Клейна.

Рассмотрим на евклидовой плоскости некоторую окружность с центром О радиуса r = 1 и назовем ее абсолютом. Обозначим через круг с границей , а через множество внутренних точек этого круга.

Введем следующие соглашения. Неевклидовой точкой назовем любую евклидову точку М , а неевклидовой прямой — любую хорду (без концов) окружности . Отношения «принадлежность» и «лежать между» понимаем в обычном смысле. Неев­клидовы прямые будем обозначать так: UV, U₁V₁ и т.д., предполагая, что U, V, U₁, V₁ . Таким образом, неевклидовыми точками прямой UV будут те и только те евкли­довы точки, которые лежат между точками U и V.

Нетрудно убедиться в том, что при этих соглашениях выполняются все аксиомы I_1-3, II_1-4 Гильберта. Проверим в качестве примера аксиому II₂(см. §71). Пусть А и В - две неевклидовы точки, а UV — неевклидова прямая, на которой они лежат. Так как А и В - внутренние точки хорды UV, то на этой хорде существует хотя бы одна внутренняя точка С, такая, что А — В — С. Отсюда мы заключаем, что сущест­вует по крайней мере одна неевклидова точка С, такая, что неевклидова точка В лежит между неевклидовыми точками А и С.

Так как в построенной модели выполняются все аксиомы групп I, II Гильберта, то выполняются и все следствия из этих аксиом, в частности имеют место теоремы, с по­мощью которых вводятся понятия луча и полуплоскости. Ясно, что неевклидовым лучом, исходящим из точки С, является множество всех внутренних точек произ­вольной полухорды CU окружности (CU — евклидов отрезок, где С — внутренняя точка круга , а U — точка на его границе). Неевклидовой полуплоскостью является множество всех внутренних точек какого-нибудь сегмента круга .

2. Для того чтобы в нашей модели определить равенство отрезков и углов, введем ряд вспомогательных понятий. Напомним, что на евклидовой плоскости про­стым отношением трех точек А, В и С, лежащих на одной прямой, называется число

(АВ, С) = , такое, что АС = С В, а сложным отношением четырех точек А, В, С, D, лежащих на одной прямой, - число (АВ, СD)= . Из этого определения непосредственно вытекают следующие свойства.

1°. Если (AB, CD) = (АВ, CD'), то точки D и D' совпадают.

2°. Для любых четырех точек А, В, С, D прямой имеем (АВ, CD) = (CD, АВ) =

=(ВА, DC) = (DC, ВА).

Если четыре точки на прямой заданы своими координатами М₁(x₁, у₁), M₂(x₂, y₂), М₃ (x₃, y₃) и M₄ (х₄, у₄), то

(М₁М_2, М₃М₄)= 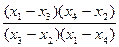= . (1)

Одна из этих формул теряет смысл, если данные точки лежат на прямой, парал­лельной одной из координатных осей.

Биективное отображение назовем -преобразованием, если выполнены следующие условия.

а) Внутренние точки круга переходят во внутренние точки этого же круга, а граничные точки этого круга — в граничные точки.

б) Любая хорда окружности переходит в некоторую хорду этой же окружности, и при этом сохраняется сложное отношение соответственных точек.

Рассмотрим примеры - преобразований.

Пример 1. Любое движение евклидовой плоскости, имеющее центр абсолюта своей инвариантной точкой, индуцирует во множестве некоторое - преобразование. В частности, тождественное преобразование множества , вращение вокруг центра О круга , отражение от любого диаметра круга являются примерами - преобразо­ваний.

Пример 2. Пусть отображение в системе координат Оху задано формулами

х^/= , у^/= , где <1. (2)

Так как для точек множества -1 х 1, то 1- ax 0, поэтому каждая точка множества имеет образ. Из формул (2) получаем:

х^{/ 2} – у^{/ 2} = , (3)

х= , у= .

Из равенства (3) следует, что точки абсолюта о) при отображении f переходят в точки абсолюта, а точки множества - в точки того же множества . Далее, из равенств (4) мы заключаем, что каждая точка (х^/, у^/) множества имеет единственный прообраз (х, у), поэтому отображение (3) является биекцией множества .

Отметим, что преобразование f, как показывают формулы (2) и (4), является инволютивным, т. е. f ^-1 = f.

Докажем, что для преобразования выполняются также условия б). Если точки М₁, M₂, М₃ лежат на прямой Ах + By + С = 0, то, используя формулы (4), мы убеждаемся в том, что их образы М^/₁, M^/₂, М^/₃ также лежат на некоторой прямой. Таким образом, если UV— некоторая хорда окружности , а U^/ = f(U), V^/ = f(V), то все точки хорды UV переходят в точки хорды U^/V^/. Но так как f^-1= f, то все точки хорды U^/V^/ переходят в точки хорды UV. Таким образом, хорда UV переходит в хорду U ^/V^/.

Остается доказать, что преобразование (2) сохраняет сложное отношение четырех точек. Пусть М₁(х₁, у₁), М ₂(х₂, y₂), М ₃(x₃, у₃), М₄ (x₄, у₄) — четыре точки, лежащие на одной прямой, пересекающей ось Оу, a М^/_i(x^/_i, y^/_i), i = 1, 2, 3, 4,— их образы. Используя первую из формул (4), находим:

x_i – x_j - ,

где i, j = 1, 2, 3, 4, i j.

Отсюда, применяя формулу (1), получаем (M₁,M₂,М₃,М₄) = (M^/₁M^/₂,M^/₃M^/₄). Если точки М_i лежат на прямой, параллельной оси Оу, или на оси Оу, то, исполь­зуя вторую из формул (4), приходим к тому же выводу.

Итак, доказано, что формулами (2) задано инволютивное - преобразование.

3. Рассмотрим некоторые свойства - преобразований. Из определения -преобразования непосредственно следует утверждение.

1°. Если f и g - - преобразования, то fg и f ^-1 являются - реобразованиями.

2°. Любое - преобразование сохраняет отношение «лежать между» точек круга .

Доказательство:

Пусть А, В, C и А — В—С, а А^/, В^/ С^/— образы этих точек. Обозначим через UV хорду, на которой лежат данные точки, а через U ^/V ^/образ этой хорды. Если точки А и С являются концами хорды UV (т.е. совпадают с точками U и V), то А^/ и С^/ являются концами хорды U ^/V^/. В этом случае утверждение 2⁰ очевидно. Предпо­ложим, что точка U не совпадает ни с одной из точек А и С. Тогда (AC, BU) = (А^/С^/,В^/U^/) или = . Так как (AC, U)< О, (А ^/С^/, U^/) < 0 и по условию (АС, В) > 0, то из последнего равенства следует, что (А 'С', В') > 0. Это означает, что А^/ - В^/ - C^/.

Отсюда мы заключаем, что при - преобразований отрезок, принадлежащий кругу , переходит в отрезок; в частности, полухорда круга переходит в полухорду того же круга. Далее, любой сегмент круга ^ переходит в сегмент того же круга.

Пусть UV — хорда круга , AU — полухорда этой хорды, а — один из сегмен­тов, ограниченный хордой UV. Пару AU, назовем - флагом и обозначим через (AU, ). На рисунке 239 изображены два - флага (A ₁ U ₁, ₁) и (A ₂U₂, ₂)- Из предыду­щего ясно, что - преобразование любой - флаг переводит в - флаг.

Доказательство завершено.

3°. Какова бы ни была внутренняя точка А круга , существует инволютивное -преобразование, которое переводит точку А в центр О круга , а точку О в точку А.

Доказательство:

В самом деле, пусть ОА = а. Выберем прямоугольную систему координат Оху так, чтобы точка А в этой системе имела координаты А (а, 0). Тогда -преобразо­вание, заданное формулами (2), переводит точку А в точку О, а точку О в точку А.

Доказательство завершено.

4°. Каковы бы ни были флаги I₁ ==(A₁U₁, ₁)и I₂ =(А₂U₂, ₂), существует - преобразование, которое I₁ переводит в I₂(рис. 239).

Доказательство:

По свойству 3° существуют инволютивные -преобразования f₁ и f₂, такие, что О = f₁(A₁) и О = f₂(А₂), где О — центр круга . Пусть I^/₁ = f¹(I₁) и I^/₂= f₂(I₂)- Рас­смотрим -преобразование f₀, такое, что I ^/₂ = fo(I^/₁) (fo является вращением вокруг точки О или вращением вокруг точки О с последующим отражением от диаметра круга ). Тогда f == f ₂f₀f₁ является искомым - преобразованием, так как f(I₁)=f₂f₀f₁(I₁)=f₂f₀(I^/₁)=f₂(I^/₂)=I₂.

Отсюда, как следствие, получаем утверждение.

Доказательство завершено.

5°. Каковы бы ни были полухорды A₁U₁ и A₂U₂, существует -преобразование, которое полухорду A₁U₁ переводит в полухорду А₂U₂.

Сформулируем еще одно свойство, которое мы приводим без доказательства.

6°. Если - преобразование какой-нибудь - флаг переводит в себя, то оно является тождественным преобразованием круга .

4. В этом пункте для простоты изложения неевклидовы отрезки, лучи, углы, полуплоскости будем называть просто отрезками, лучами, углами, полуплоскостями. Введем следующие соглашения. Будем считать, что отрезок АВ равен отрезку А^/ В^/, если существует такое - преобразование, которое отрезок АВ переводит в отрезок А ^/В^/. Аналогично угол hk считается равным углу h ^/k^/, если существует - преобразование f, которое угол hk переводит в угол h ^/k^/ (т. е. h^/ = f(h) и k^/ = f(k) или k^/ = f{h) и h ' = f(k)).

Заметим, что если hk == h ^/k^/, то всегда найдется такое - преобразование f^/, что h ' = f^/(h), k^/ = f^/(k). В самом деле, допустим, что равенство hk = h ^/k^/ озна­чает существование такого - преобразования, что k^/ = f(h), h^/ = f(k). Рассмотрим инволютивное -преобразование f₁, которое вершину угла hk переводит в центр О круга (свойство 3°). Пусть h₁= f₁(h), k₁ = f₁(k). Если f₂ симметрия с осью, содержащей биссектрису угла h₁k₁, то k₁ == f₁(h₁), h₁ = f₂(k₁). Поэтому f ^/= ff 1f ₂f₁ является искомым - преобразованием.

Покажем, что все аксиомы группы III Гильберта выполнены.

III₁. Пусть АВ — данный отрезок, отложенный на луче h, a h^/- луч, исходящий из точки А^/. Докажем, что существует точка B^/ h^/, такая, что А ^/В^/= АВ.

Обозначим через AU и A ^/U^/ полухорды круга , на которых лежат лучи h и h^/, а через UV и U ^/V ^/ соответствующие хорды. Рассмотрим - преобразование f, которое полухорду AU переводитв полухорду А^/U^/ (свойство 5°). Тогда h^/ = f(h). Если В^/ = f(B), то B ^/ h^/, и по определению А ^/В^/ = АВ.

Замечание. В нашей модели на луче h' существует единственная точка В ^/, удовлетворяющая условию АВ = А ^/В^/. В самом деле, U ^/ = f(U ^/), V ^/ = f(V ^/), поэтому (UV, АВ) = (U ^/ V ^/, А ^/В^/). Если допустить, что на луче h' существует другая точка В^// такая, что АВ = А ^/В ^//, то аналогично получаем (UV, АВ) =(U ^/V ^/, А ^/В ^//). Поэтому (U ^/ V ^/, А ^/В^/) = (U ^/V ^/, А ^/В ^//). По свойству 1⁰ сложного отношения четырех точек точки В^/ и В ^// совпадают.

III₂. Выполнение этой аксиомы непосредственно следует из свойства 1⁰ Λ - пре­образований.

III₃. Пусть А - В - С, А^/ - В^/ - С^/, АВ = А^/ В^/ и ВС = В ^/С^/. Докажем, что АС = А ^/С ^/. Рассмотрим полухорды BU₁, BU₂, B ^/U ₁^/, B ^/U^/₂, на которых лежат соответ­ственно точки А, С, А^/ и С ^/ (рис. 240, а). По свойству 5° существует такое Λ - преобра­зование f, которое полухорду BU₁ переводит в полухорду B ^/U ₁^/. При этом полухорда BU₂ переходит в полухорду B ^/U^/₂. Пусть A₁ = f(A), C₁ = f(C).

Так как ВА = B ^/A^/ по условию и ВА = B ^/A₁ по построению, то точки А^/ и A₁ совпадают, т. е. А^/= f(A) (см. замечание к аксиоме III ₁). Аналогично доказывается, что точки С^/ и С₁ совпадают, поэтому С ^/ = f(C). Таким образом, Λ - преобразование f отрезок АС переводит в отрезок А ^/С ^/, т.е. АС = А ^/С ^/.

III₄. Пусть даны угол hk и флаг (А ^/, h^/, ^/). Докажем, что существует единствен­ный луч k^{/ /}, такой что hk = h ^/k^/. Для этого рассмотрим Λ -флаги I = (AU, ) и

I' = (A ^/U^/, ^/), которые выбраны так, что h AU, h^/ A ^/U^/, k , ^/ . По свой­ству 4° существует такое Λ - преобразование f, что I ^/ = f(I). Луч k^/ = f(k) является искомым, так как k^{/ /}, и по определению равенства углов hk = h ^/k^/.

Предположим, что k^// - луч, удовлетворяющий условиям: hk = h ^/k ^// и k ^// I ^/. Тогда, очевидно, h ^/k^/ = h ^/k^//, поэтому существует такое Λ -преобразова­ние f, что

h^/ = f(h^/), k^// = f(k^/). Отсюда мы заключаем, что преобразование f Λ - флаг I ^/ переводит в себя. По свойству 6⁰ f - тождественное преобразование круга , следо­вательно, лучи h ^/ и k ^// совпадают.

III₅. Пусть в треугольниках АВС и A ^/B ^/C ^/ имеем АВ = А ^/В^/, АС = А ^/С^/ и ВАС = B ^/A ^/C ^/. Докажем, что AВС = A ^/B ^/C^/.

Так как ВАС = B ^/A ^/C ^/, то существует такое Λ - преобразование f, которое переводит луч АВ в луч А ^/В^/, а луч АС в луч А ^/С ^/. Пусть B₁ = f(B) и C₁ = f(C). Так как А ^/= f(A), то АВ = A ^/B₁. Но по условию АВ = А ^/В ^/, поэтому точки B₁ и В ^/ совпа­дают, т.е. В ^/= f(B) (см. замечание к аксиоме III ₁). Аналогично доказывается, что С ^/ = f(C). Таким образом, Λ -преобразование f точки А, В, С переводит соответственно в точки А ^/, В ^/, С ^/, поэтому ABC= A ^/B ^/C ^/.

IV₁ и IV₂. Группа IV аксиом Гильберта эквивалентна предложению Дедекинда. Ясно, что предложение Дедекинда выполняется на построенной нами модели, поэтому выполняются аксиомы IV₁ и IV₂ Гильберта.

V*. Возьмем произвольную прямую UV и точку А, не лежащую на ней. Рас­смотрим прямые UU₁ и VV₁, проходящие через точку А (рис. 240, б). Эти прямые не пересекаются с прямой UV, так как евклидовы точки U и V не являются неевклидо­выми точками прямой UV. Таким образом, имеет место аксиома V* Лобачевского.

5. Таким образом, построив евклидову модель Кэли — Клейна, мы тем самым дока­зали, что система аксиом I_1-3, II_1-4, III_1-5, IV_1-2, V* непротиворечива, если непро­тиворечива система аксиом 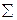_н Гильберта. (Непротиворечивость системы аксиом 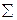_н будет доказана ниже, в § 83.) Отсюда непосредственно следует, что аксиома парал­лельных V не зависит от аксиом I_1-3, II_1-4, III_1-5, IV_1-2 Гильберта. Но выше было доказано, что аксиома параллельных V эквивалентна V постулату Евклида, поэтому V постулат Евклида не зависит от остальных аксиом евклидовой планиметрии.

[1] В некоторых изданиях “Начал” Евклида V постулат включен в число аксиом и называется XI аксиомой.

[2] См. Гильберт Д. Основания геометрии. – М.: ГИТТЛ, 1948.

[3] Напомним, что когда мы говорим «две точки», «три прямые», то предполагаем, что эти точки или прямые попарно различны.

[4] Напомним, что если О' — некоторая точка, h' — луч, исходящий из этой точки, а 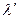- полуплоскость с границей 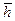, то тройка называется флагом ().

[5] Интересно отметить, что для введения понятия площади или объема необходимо к аксиомам групп I – IV добавить аксиому параллельности, то есть рассматривать все аксиомы евклидовой геометрии.

[6] Внутренним лучом данного угла называется луч, исходящий из вершины угла и целиком принадлежащий внутренней области угла.

[7] Интересно отметить, что прямые, содержащие высоты треугольника на плоскости Лобачевского, не всегда пересекаются в одной точке.

[8] См.: Новиков П.С. Элементы математической логики. – М.: Наука, 1973.

1 Cм.: Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия: Пробный учебник для 6 класса средней школы.- М.: Просвещение,1984.

1 См. приложение «Об аксиомах планиметрии» в учебнике Л. С. Атанасян а, В. Ф. Бутузова, С. Б. Кадомцева, Э. Г. Позняка «Геометрия, 7» (4-е изд.— М.: Просвещение, 1986). Полный список аксиом пространства Е₃ помещен в приложении к пробному учебнику тех же авторов «Геометрия, 9—10» (3-е изд.— М.: Просвещение, 1987).