Об аксиомах школьного курса геометрии

1. В основу дедуктивного построения школьного курса геометрии можно положить различные системы аксиом. Например, до введения в школу учебного пособия по геометрии А. В. Погорелова в VI—VIII классах средней школы планиметрия изучалась по учебному, пособию под редакцией А. H. Колмогорова. В системе аксиом планиметрии этого пособия база структуры евклидовой плоскости состоит из трех множеств: Е, F и G, где Е - множество точек, F - множество прямых и G - множество некоторых неотрицательных величин, которые называются расстояниями. Основными отношениями являются отно­шение принадлежности точек и прямых и тернарное отношение, которое определяется отображением &: Е X Е 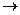G. Мы не будем формулировать аксиомы А. H. Колмогорова; читателя, интересующегося этим вопросом, отсылаем к книге [4] (раздел IV, § 19).

В последние годы издан ряд пробных учебников по геометрии для средней школы, в которых курс геометрии строится также дедуктивно на основе той или иной системы аксиом. Оригинальная аксиоматика положена в основу курса геометрии в пробных учебниках геометрии А. Д. Александрова, А. Л. Вернера и В. И. Рыжика 1. В системе аксиом, данной в этом учебнике, база структуры евклидовой плоскости состоит из двух множеств - множества точек и множества отрезков, а прямая определяется с помощью отрезков.

Система аксиом, положенная в основу курса геометрии в пробных учебниках Л. С. Атанасяна, В. Ф. Бутузова, С. Б. Кадомцева, Э. Г. Позняка, аналогична системе аксиом Гильберта. База структуры состоит из тех же множеств Е, F, G, что и база структуры евклидова прост­ранства по Гильберту (Е — множество точек, F — множество прямых, a G — множество плоскостей; см. пример 2 § 11). Основными отноше­ниями в системе множеств Е, F, G являются, как и у Гильберта, отно­шения ₁, ₂, которые обозначаются словами «лежит на», «лежит между», но вместо отношения ₃ («равенство отрезков и углов») вводится новое отношение ₃^* («наложение»). Это отличие является существенным, так как вместо аксиом конгруэнтности Гильберта фор­мулируются другие аксиомы (аксиомы наложения), и поэтому все определения и теоремы о равенстве фигур вводятся и доказываются не так, как по схеме Гильберта.

2. Рассмотрим более подробно аксиоматику планиметрии, данную в пробных учебниках геометрии Л. С. Атанасяна и др. 1

База структуры евклидовой плоскости E ₂ состоит из двух множеств: Е (множество точек) и F (множество прямых). Основными отношениями являются следующие три отношения: а) «принадлежать» для точек и прямых; б) «лежать между» для трех точек одной прямой (если точка В лежит между точками A и С, то мы запишем так: А—В—С); в) «наложение», т. е. бинарное отношение, которое определяется отображением f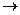: Е Е.

Система аксиом, которую мы здесь приводим, в основном совпадает с аксио­матикой школьного курса, но по сравнению с ней несколько ослаблена. Введение в школьный курс дополнительных предложений в виде аксиом вызвано методическими соображениями.

Рассматриваемая система аксиом, которую обозначим через _A, состоит из пятнадцати аксиом, разбитых на пять групп.

1. Аксиомы принадлежности.

I₁. Каковы бы ни были две точки, существует прямая, проходящая через эти точки, и притом только одна.

II₂. На каждой прямой лежат по крайней мере две точки. Существуют по крайней мере три точки, не лежащие на одной прямой.

II. Аксиомы порядка.

II₁. Если А—В—С, то А, B и С— различные точки одной прямой и С—В—А.

II₂. Каковы бы ни были точки А и В, существует по крайней мере одна точка С, такая, что А—В—С.

II₃. Среди трех точек прямой существует не более одной точки, лежащей между двумя другими.

На основании этих аксиом вводится понятие отрезка. Отрезком АВ называется множество, состоящее из точек А, В и всех точек, лежащих между ними. Говорят, что точки А и В лежат по одну сторону (по разные стороны) от прямой а, если отре­зок АВ не имеет общих точек с прямой а (отрезок AB имеет только одну общую внутреннюю точку с прямой а).

II₄. Каждая прямая разбивает множество всех точек плоскости, не лежащих на этой прямой, на два подмножества (полуплоскости) так, что любые две точки одного и того же подмножества лежат по одну сторону от данной прямой, а любые две точки разных подмножеств лежат по разные стороны от этой прямой.

Пользуясь этими аксиомами, вводится понятие луча и доказывается теорема о дополнительных лучах, которая в учебнике средней школы из методических сообра­жений принята как аксиома (аксиома 5). Затем вводится понятие угла: фигура, состоящая из точки и двух лучей, исходящих из этой точки, называется углом. Угол называется развернутым, если эти лучи лежат на одной прямой.

III. Аксиомы наложения.

III₁. Наложение есть инъективное отображение плоскости в себя.

III₂. Если при наложении точки А, М, В переходят соответственно в точки А^/, М^/, В^/ и А— М— В, то А^/— М^/ — В^/.

Фигура Ф называется равной (конгруэнтной) фигуре Ф ^/, если существует нало­жение, при котором фигура Ф переходит в фигуру Ф ^/. Запись Ф = Ф ^/ означает, что фигура Ф равна фигуре Ф ^/.

Фигуру, состоящую из двух точек А и В, обозначим через {А, В}.

III₃. Если {А^/, В^/} = {А, В} и {A ^//B^//}= {А, В}, то {А^/, В^/} ={A ^//B^//}.

III₄. Если даны пара точек {A, В} и луч h, исходящий из точки А^/, то существует одна и только одна точка В^/ луча h, такая, что = {А, В } = {А^/, В^/}.

Пользуясь этими аксиомами, можно доказать ряд теорем об образах фигур при наложении: при любом наложении отрезок переходит в отрезок, луч переходит в луч, угол переходит в угол, причем неразвернутый угол — в неразвернутый угол. Таким образом, можно говорить о равенстве углов: угол hk называется равным углу h ^/k^/, если существует наложение f, такое, что f (h) = h^/ и f (k) = k^/ или f (h) = k^/ и f (k) = h^/.

III₅. Если даны неразвернутый угол hk и флаг (О^/, h^/, ^/), то существует один и только один луч k^/ полуплоскости ^/, исходящий из точки О ^/, такой, что hk = h ^/k^/. Каждый угол равен самому себе.

III₆. Если неразвернутый угол hk равен углу h ^/k, то существует наложение, при котором луч h переходит в луч h^/, а луч k — в луч k^/, и наложение, при котором луч h переходит в луч k^/, а луч k — в луч h^/.

Пользуясь этими аксиомами, можно доказать ряд теорем, которые из методиче­ских соображений в пробном учебнике для средней школы приняты в качестве аксиом (аксиомы 8, 12, 13 и 14).

Движением назовем любую биекцию плоскости, при которой любая пара {А, В} переходит в равную пару {А^/, В^/}. Пользуясь аксиомами групп I, II и III, можно до­казать, что понятия наложения и движения совпадают.

IV. Аксиомы непрерывности.

IV₁ (аксиома Архимеда), Пусть АВ и CD— какие-нибудь отрезки. Тогда на прямой АВ существует конечное множество точек A₁, А₂,..., A_n, таких, что выполняют­ся условия:

а) A—A₁— A₂, A ₁— A₂ — A₃,..., A _n-2— A_n-1 — A_n,

б) AA₁, =A ₁A₂ =... = A _n-1,A _n = CD.

в ) A --В—A _n.

Следствием из аксиом, перечисленных выше, является теория измерения отрез­ков (см. гл. XI). В частности, можно доказать, что, выбрав единичный отрезок, мож­но измерить любой отрезок способом, известным из курса средней школы. Таким образом, каждому отрезку ставится в соответствие положительное число так, что рав­ным отрезкам соответствует одно и то же число, и если A — В—С, то отрезку АС соот­ветствует число, равное сумме чисел, соответствующих отрезкам АВ и ВС. В пробном учебнике это утверждение выражено в аксиоме 15.

IV₂. Для любого положительного вещественного числа d существует отрезок, длина которого при выбранном единичном отрезке равна d.

Аксиома параллельных прямых.

V. Через точку, не лежащую на данной прямой, в плоскости, определяемой пря­мой и точкой, проходит не более одной прямой, параллельной данной.

2. В этой главе было показано, что все аксиомы групп I, II, IV и V выполняются в теории Г ( _W). Так как любое наложение есть движение, то в этой теории выполняют­ся аксиомы группы III. Поэтому имеет место теорема, аналогичная теореме § 84.

Теорема. Система аксиом _A непротиворечива, если непротиворечива арифме­тика вещественных чисел.