Непротиворечивость, независимость и полнота системы аксиом

1. Как было отмечено выше, система аксиом называется непротиво­речивой, если существует база, на которой можно задать рассматри­ваемую структуру рода Т. Чтобы доказать непротиворечивость систе­мы аксиом, достаточно построить какую-либо интерпретацию это^ системы аксиом. При построении интерпретации мы должны использовать «достаточно надежные» понятия, относительно которых у нас есть уверенность, что их система внутренне непротиворечива. Только в этом случае можно утверждать, что наша система аксиом А ₁, А₂,…А_t внутренне непротиворечива, и, значит, в теории Г(Т) мы не получим двух теорем, отрицающих одна другую, как бы далеко мы ни развивали эту теорию.

Если система аксиом А₁, А₂,…, А_t противоречива (Т = Ø), то она не определяет никакой структуры: не существует множеств Е, F, G (базы), таких, чтобы какие-либо отношения на них обладали свойст­вами А₁, А₂,…А_t. Следовательно, такая система аксиом бесполезна.

Таким образом, система аксиом А₁, А₂,..., А_t, для которой мы собираемся строить теорию Г (Т), должна быть непротиворечивой. Это важнейшее требование, предъявляемое ко всякой системе аксиом.

Как уже отмечалось выше, вопрос о внутренней непротиворечивости системы аксиом может быть решен только средствами математической логики.

При построении интерпретаций систем аксиом, определяющих структуры, изучаемые в геометрии, мы используем различные числовые множества, считая «наиболее надежными» понятия, взятые из арифметики вещественных чисел. Поэтому при исследовании непротиворечивости системы аксиом А₁, А₂,..., A_t, не прибегая к средствам математической логики, мы в лучшем случае можем прийти к утверждению такого вида: система аксиом А₁, А₂,..., А_t непротиворечива, если непротиворечива арифметика вещественных чисел.

Пример 1. Докажем, что группа I аксиом Гильберта непротиворечива. Для этого построим интерпретацию системы {I₁, I₂,..., I₈}. Возьмем какое-нибудь множество , состоящее из четырех элемен­тов а, b, с, d (пусть, например, a, b, c и d— различные числа). Точкой назовем каждый элемент этого множества; прямой— каждое из подмножеств, состоящее из двух элементов, т. е. {а, b}, {а, с}, {а, d}, {b, с}, {b, d}, {с, d} — прямые; плоскостью — каждое из подмножеств, со­стоящее из трех элементов, т. е. {а, b, c}, {а, с, d}, {а, b, d} и {b, с, d}— плоскости. Будем говорить, что точка лежит на прямой (или на пло­скости), если соответствующий элемент множества принадлежит соответствующему подмножеству. Например, точка а лежит на пря­мой { а, с }, но не лежит на плоскости {b, с, d}. Предлагаем читателю самостоятельно убедиться в том, что при этих соглашениях выполняются все аксиомы группы I Гильберта.

2. Мы знаем, что система аксиом = { А₁, А₂,..., А_t } представляет собой перечень явно сформулированных требований, которым долж­ны удовлетворять отношения

₁, ₂,..., _k на множествах Е, F, G базы.

Пусть система аксиом непротиворечива, и, значит, можно стро­ить теорию Г (Т) структур рода Т. Возникает вопрос: все ли аксиомы системы необходимы для определения данного рода структур, т. е. нельзя ли число этих аксиом уменьшить, не меняя T?

Пусть А — одна из аксиом системы . Аксиома А называется зависимой от остальных аксиом системы , если предложение А яв­ляется логическим следствием из остальных аксиом системы . В этом случае аксиома А выполняется, как только выполняются аксиомы системы ^/ = \ {А}. Ясно, что в этом случае любая интерпретация системы ^/ является также интерпретацией и системы (т. е. ^/ опре­деляет то же множество Т).

В системе заменим аксиому А ее отрицанием Ā (не А) и обозна­чим новую систему аксиом через *, т. е. * = ^/ {Ā}. Всякая интер­претация системы * служит также интерпретацией и системы '. Если аксиома А зависима от остальных аксиом системы , то она должна выполняться в интерпретации системы *, в которой выполняется и аксиома Ā. Но любое отношение _i, не может обладать свойства­ми A и Ā одновременно. Следовательно, если аксиома А зависима от остальных аксиом системы , то система аксиом * противоречива (не существует ее интерпретаций).

Таким образом, чтобы доказать независимость аксиомы А от остальных аксиом системы , достаточно доказать, что система * содержательно непротиворечива.

Система аксиом, определяющая структуру абеле­вой группы, состоит из аксиом А₁ —А₄ (§ 11, пример 1) и следующей аксиомы:

A₅: для любых двух элементов а, b из Е имеем (a, b) = (b, а).

Докажем, что аксиома A₅ независима от аксиом A₁ - А₄.

Для этого достаточно доказать непротиворечивость системы ак­сиом 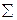* = {A₁, А₂, А₃, А₄, Ā₅}, где Ā₅ — отрицание аксиомы A₅.

Ā₅: существует хотя бы одна пара элементов из Е, таких, что (a, b) (b, a).

Непротиворечивость системы * следует из того, что существуют некоммутативные группы (например, мультипликативная группа не­вырожденных квадратных матриц порядка п 2 над полем R).

Пример 3. Рассмотрим группу I аксиом Гильберта (см. при­мер 1) и докажем, что аксиома I₁ не зависит от аксиом I₂—I₈. Для этого достаточно доказать непротиворечивость системы аксиом

* = {Ī₁, I₂ I₃,..., I₈}, где Ī — отрицание аксиомы I₁: существуют по крайней мере две точки, через которые не проходит ни одна прямая.

Докажем, что система * непротиворечива. Для этого несколько видоизменим интерпретацию, рассмотренную в примере 1. Точки и плоскости интерпретируются так же, как и в примере 1, а прямыми назовем следующие пять подмножеств: {а, с}, {a, d}, {b, с}, {b, d] и {с, d}. Ясно, что при этом выполняются все аксиомы системы *: ак­сиома Ī₁ выполняется, так как через точки а и b не проходит ни одна прямая; выполнение аксиом I₂- I₈ очевидно.

Если аксиома А зависима от остальных аксиом системы , то ее можно вычеркнуть из списка аксиом и строить теорию Г(Т), поль­зуясь лишь аксиомами системы ^/ = \{A}.

Конечно, желательно иметь такую систему аксиом , в которой каждая аксиома независима от остальных. Такая система аксиом называется независимой. В некоторых случаях удается получить такую систему, вычеркивая из данной системы последовательно те аксиомы, которые зависимы от остальных.

Но данная система может быть такой, что для некоторых ее аксиом даже бессмысленно ставить вопрос, об их зависимости или независимости от остальных. Так обстоит дело в аксиоматике Гиль­берта. Нельзя говорить о независимости некоторых аксиом Гильберта потому, что от их содержания зависит ряд других аксиом. Бессмыс­ленно ставить вопрос о независимости аксиомы Паша от всех осталь­ных аксиом, так как для самой формулировки, например, аксиом конгруэнтности мы должны иметь понятия луча и полуплоскости, а эти понятия вводятся на основании аксиомы Паша. Поэтому если мы исключим из рассмотрения аксиому Паша, то некоторые ак­сиомы группы III не могут быть сформулированы.

З а м е ч а н и е. Если аксиома А независима от остальных ак­сиом системы , то система * непротиворечива и определяет струк­туры рода Т*, отличные от структур рода Т, определяемых систе­мой . Именно с таким случаем мы имеем дело при рассмотрении системы аксиом Гильберта _H = {I, П, III, IV, V} и системы аксиом геометрии Лобачевского _Л ={I, II, III, IV, V*}, где V*—аксиома Лобачевского, которая представляет собой отрицание V постулата. Как будет выяснено позже, обе системы аксиом _H и _Л непротиво­речивы.

3. Пусть дана непротиворечивая система аксиом , описывающая свойства отношений ₁, ₂..., _k. Допустим, что существует ак­сиома А, которая удовлетворяет условиям:

а) аксиома А сформулирована в терминах теории Г (), и, следо­вательно, она не вводит новых отношений;

б) аксиома А независима от аксиом системы ;

в) система аксиом U {А} непротиворечива.

В этом случае система аксиом называется неполной (точнее, дедуктивно неполной). Если же такой аксиомы А не существует, то система называется полной (дедуктивно полной).

Пусть система аксиом неполная, и, значит, существует ак­сиома А, удовлетворяющая указанным выше условиям а), б), в). По условию в) система аксиом ^/= {А} непротиворечива, а так как А не зависит от аксиом системы (по условию б)), то непроти­воречива и система аксиом ^//= U {Ā}. Обозначим через М^/, М^// ка­кие-либо интерпретации систем ^/, ^//соответственно. Так как ^/ и ^//, то М ^/ и М ^// являются также интерпретациями и системы аксиом .

Но в интерпретации М^/ выполнена аксиома А, а в М^// — Ā (не А), и, следовательно, интерпретации М^/ и М^// (системы ) не изоморфны. (Если предположить, что интерпретации М^/ и М^// изоморфны, то мы получим, что основные отношения ₁,..., _k должны обладать одно­временно как свойствами {а₁,..., А_t, А}, так и свойствами {А₁,..., A_t, Ā), что, конечно, невозможно.) Таким образом, если система аксиом неполная, то для нее существуют неизоморфные интерпретации.

Из определения полной (неполной) системы аксиом следует, что всякая непротиворечивая система аксиом либо является полной, либо неполной. Поэтому если все интерпретации системы аксиом изоморфны (такую систему аксиом часто называют категоричной), то эта система заведомо полная. Но отсюда никак не следует, что если система аксиом дедуктивно полная, то она будет и категорич­ной.

Мы приходим к такому выводу: чтобы доказать, что данная си­стема аксиом полная, достаточно доказать, что все ее интер­претации изоморфны.

Пример 4. Тот факт, что к системе аксиом A₁-A₄, опреде­ляющей структуру группы, можно добавить независимую от этих аксиом аксиому A₅, которая не вводит новых отношений, и при этом получается непротиворечивая система А₁-A₅ (определяющая струк­туру абелевой группы), дает возможность заключить, что система аксиом A₁—A₄ групповой структуры неполная.

Пример 5. Рассмотрим систему аксиом абсолютной геометрии, т. е. систему = {I, II, III, IV}, состоящую из первых четырех групп аксиом Гильберта. Эта система является неполной, так как к ней можно добавить независимую от аксиом этой системы аксиому V па­раллельности и при этом получается непротиворечивая система _H.

Пусть система аксиом непротиворечива и определяет структуры рода Т. Если все эти структуры изоморфны (т. е. система аксиом категоричная), то говорят, что теория Г(Т) однозначна. Если же не все структуры рода Т изоморфны (т. е. система аксиом некатегорич­ная), то говорят, что теория Г(Т) многозначна. В современной математике нередко встречаются многозначные теории (например, теория групп).

З а м е ч а н и е. Дедуктивную полноту системы аксиом иногда определяют иначе. Пусть система аксиом дедуктивно неполная в смысле данного выше определения. Что можно сказать о предло­жении А? Из условия а), указанного в определении, мы знаем, что предложение А сформулировано в терминах теории Г (). Из усло­вия б) следует, что предложение А недоказуемо в теории Г () (т. е. его нельзя вывести как логическое следствие аксиом ). Из условия в) заключаем, что и предложение Ā (не А) недоказуемо в этой теории.

Говорят, что предложение А опровержимо, если Ā доказуемо. Мы приходим к такому определению: система аксиом называется дедуктивно неполной, если существует предложение А, сформулиро­ванное в терминах теории Г (), которое недоказуемо и неопровер­жимо в данной теории.

Если же для всякого предложения А, сформулированного в тер­минах понятий теории Г (), оказывается доказуемым либо это предложение, либо его отрицание Ā, то система аксиом является дедуктивно полной.