 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие о математической структуре
|
|
1. Напомним понятие отношения. Пусть даны непустые множества М1, M2,..., Мn. Всякое подмножество Δ  М1
М1 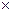 М2
М2 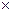 ...
... 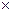 Мn называется n -арным (или n -местным) отношением, определенным во множествах М1, M2,..., Мn. Говорят, что элементы m1, m2,..., m n (m i
Мn называется n -арным (или n -местным) отношением, определенным во множествах М1, M2,..., Мn. Говорят, что элементы m1, m2,..., m n (m i  Mi) находятся в отношении Δ, если (m1, m2,..., mn)
Mi) находятся в отношении Δ, если (m1, m2,..., mn)  Δ.
Δ.
Если М1= M2=...= Мn= М и, следовательно, М1 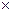 М2
М2 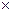 ...
... 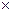 Мn = Мn (n -я декартова степень множества М), то говорят, что n -арное отношение Δ
Мn = Мn (n -я декартова степень множества М), то говорят, что n -арное отношение Δ  М n определено во множестве М.
М n определено во множестве М.
В случае бинарного отношения (п = 2) Δ  М1
М1 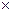 М2 вместо (m1, m2)
М2 вместо (m1, m2)  Δ. пишут:
Δ. пишут:
m1 Δ m2.
Заметим, что всякое отображение порождено некоторым отношением. В самом деле, пусть Х и Y— непустые множества и дано отображение f: Х  Y, которое каждому элементу х
Y, которое каждому элементу х  Х ставит в соответствие по некоторому закону определенный элемент f (х)
Х ставит в соответствие по некоторому закону определенный элемент f (х)  Y. Тогда определено подмножество f (X)
Y. Тогда определено подмножество f (X)  Y, состоящее из образов f (х) всех элементов х из Х (f (X) - образ множества Х в данном отображении). Обозначим Х х f (X) через Δ. Очевидно, Δ
Y, состоящее из образов f (х) всех элементов х из Х (f (X) - образ множества Х в данном отображении). Обозначим Х х f (X) через Δ. Очевидно, Δ  Х х Y, т. е. Δ - бинарное отношение, определенное во множествах Х и Y. При этом элементы х
Х х Y, т. е. Δ - бинарное отношение, определенное во множествах Х и Y. При этом элементы х  Х и у
Х и у  Y находятся в отношении Δ, если у = f (х). Говорят, что отображение f порождено отношением Δ.
Y находятся в отношении Δ, если у = f (х). Говорят, что отображение f порождено отношением Δ.
Пусть на множестве Е 

 определена алгебраическая операция (внутренний закон композиции):
определена алгебраическая операция (внутренний закон композиции):
 : Е
: Е 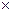 Е
Е  Е
Е
Здесь определено подмножество Δ  Е 3, образованное такими элементами (а, b, с) из Е 3, для которых
Е 3, образованное такими элементами (а, b, с) из Е 3, для которых  (а, b) = с. Мы видим, что тернарное (п = 3) отношение Δ порождает внутренний закон композиции
(а, b) = с. Мы видим, что тернарное (п = 3) отношение Δ порождает внутренний закон композиции  .
.
Рассмотрим на множестве Е внешний закон композиции со множеством операторов Λ:
g: Λ 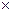 Е
Е  Е
Е
(при этом мы будем применять мультипликативную запись f (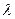 , a)=
, a)= 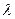 а, где
а, где 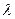
 Λ, а
Λ, а  Е). В этом случае определено подмножество Δ
Е). В этом случае определено подмножество Δ  Λ
Λ  Е
Е  E, образованное теми элементами (
E, образованное теми элементами (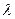 , а, b) из Λ
, а, b) из Λ  Е
Е  E, для которых
E, для которых 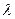 а = b. Очевидно, тернарное отношение Δ порождает внешний закон композиции g.
а = b. Очевидно, тернарное отношение Δ порождает внешний закон композиции g.
Таким образом, при помощи отношений, заданных во множествах, можно  определять как отображения одних множеств в другие, так и законы композиции на множествах.
определять как отображения одних множеств в другие, так и законы композиции на множествах.
2. Если в декартовом произведении  мы выделим два различных подмножества
мы выделим два различных подмножества  и
и  , то получим два различных отношения, определенные на системе множеств М1, М2,..., Мn. Свойства отношения
, то получим два различных отношения, определенные на системе множеств М1, М2,..., Мn. Свойства отношения  будут в чем-то отличаться от свойств отношения
будут в чем-то отличаться от свойств отношения  (так как
(так как  ).
).
Таким образом, на системе множеств М1, М2,..., Мn существует столько различных отношений, сколько различных элементов содержит множество Р(М1 х М 2х...х Мn) всех подмножеств множества М1 х М2 х…х Мn. Этих отношений будет бесконечное множество, если хоть одно из множеств Мi бесконечно. Поэтому было бы безнадежным делом ставить такую задачу: изучить свойства всевозможных отношений, которые существуют на данной системе множеств М1, М2,..., Мn.
Математика (развитие которой, как известно, определяется потребностями практики) и не ставит такой задачи. Можно сказать, что математики поступают в известном смысле наоборот: ищут и изучают множества, на которых существуют отношения с наперед указанными (нужными нам) свойствами.
3. Возьмем конечную систему различных непустых множеств. Для простоты ограничимся тройкой множеств Е, F, G. Обозначим через  1,
1,  2,…
2,…  k некоторые отношения на системе множеств Е, F, G. Эти отношения мы не будем фиксировать как определенные подмножества декартовых произведений взятых множеств, а лишь потребуем, чтобы они обладали заданными свойствами:
k некоторые отношения на системе множеств Е, F, G. Эти отношения мы не будем фиксировать как определенные подмножества декартовых произведений взятых множеств, а лишь потребуем, чтобы они обладали заданными свойствами:
А1,А2,…Аt, (1)
которые мы явно формулируем.
Может случиться, что с заданными свойствами существует не одна система отношений  , …,
, …,  (т. е. не одна система подмножеств
(т. е. не одна система подмножеств  i декартовых произведений множеств Е, F, G (j= 1, 2,..., k), а несколько). Вот простой пример.
i декартовых произведений множеств Е, F, G (j= 1, 2,..., k), а несколько). Вот простой пример.
Пусть  — алгебраическая операция на множестве R вещественных чисел (выше отмечалось, что можно рассматривать операцию
— алгебраическая операция на множестве R вещественных чисел (выше отмечалось, что можно рассматривать операцию  как отношение
как отношение 
 R 3, и мы требуем, чтобы это отношение обладало только одним свойством А1 — свойством коммутативности: для любых двух чисел а,b
R 3, и мы требуем, чтобы это отношение обладало только одним свойством А1 — свойством коммутативности: для любых двух чисел а,b  R
R  (a,b)Можно указать две коммутативные операции на множестве R (два значения отношения
(a,b)Можно указать две коммутативные операции на множестве R (два значения отношения  , обладающего свойством А1):
, обладающего свойством А1):  / — сложение и
/ — сложение и  // — умножение вещественных чисел.
// — умножение вещественных чисел.
Обозначим через Т множество всех систем  = {
= {  1,...,
1,...,  k} отношений
k} отношений  1,...,
1,...,  k, каждая из которых обладает заданными свойствами (1). Если Т
k, каждая из которых обладает заданными свойствами (1). Если Т  Ø
Ø  , то говорят, что элемент
, то говорят, что элемент  Т определяет на множествах Е, F, G структуру рода Т (точнее, математическую структуру рода Т).
Т определяет на множествах Е, F, G структуру рода Т (точнее, математическую структуру рода Т).
Явно сформулированные свойства (1), определяющие множество Т, называются аксиомами структур рода Т, а множества Е, F, G — базой структур рода Т. Всем структурам одного и того же рода дают специальное название: структура группы, структура n-мерного евклидова пространства и т. д.
Пример 1 (структура группы). В геометрии этот род структур принято определять следующим образом.
База состоит из одного непустого множества Е, система отношений состоит из одного отношения  , которое должно удовлетворять четырем аксиомам:
, которое должно удовлетворять четырем аксиомам:
А1:  — алгебраическая операция на множестве Е;
— алгебраическая операция на множестве Е;
А2: для любых элементов а, Ь, с из Е имеем  (
( (а,b) ,с) =
(а,b) ,с) =  (а,
(а,  (b, с)) {ассоциативность);
(b, с)) {ассоциативность);
А3: существует элемент е в Е, такой, что для любого а  Е имеем
Е имеем  (a, е) =
(a, е) =  (е, а) = а (существование нейтрального элемента);
(е, а) = а (существование нейтрального элемента);
А4: для любого элемента а из Е существует элемент а' из Е, такой, что  (а, а') =
(а, а') =  (а', а) = е (существование элемента а', симметричного элементу а).
(а', а) = е (существование элемента а', симметричного элементу а).
Множеству, на котором определена структура данного рода, дают специальное название. Так, в рассмотренном примере мы скажем: «Е — группа», а полностью следовало бы сказать так: «На множестве Е определена структура рода структуры группы».
Пример 2 (структура евклидова пространства по Гильберту).
По Гильберту, база структуры евклидова пространства состоит из трех множеств Е, F, G. Элементы первого множества Е называются точками, элементы множества F — прямыми, а элементы множества G — плоскостями.
На системе множеств E, F, G существуют отношения  ,
,  и
и  , которые обозначены соответственно словами «лежит на», «лежит между» и «равны». Список аксиом Гильберта состоит из двадцати аксиом: I1 – I8, II1—II4, III1—III5, IV1, IV2, V, которые сформулированы в §5, 6.
, которые обозначены соответственно словами «лежит на», «лежит между» и «равны». Список аксиом Гильберта состоит из двадцати аксиом: I1 – I8, II1—II4, III1—III5, IV1, IV2, V, которые сформулированы в §5, 6.
Эту систему аксиом коротко обозначим через  H.
H.
Пример З (структура пространства Лобачевского).
База структуры состоит из тех же трех множеств Е, F, G, что и в примере 2, элементы которых называются соответственно точками, прямыми, плоскостями.
На системе множеств Е, F, G существуют те же отношения  ,
,  ,
,  , что и в примере 2, которые обозначены соответственно словами «лежит на», «лежит между» и «равны». Список аксиом состоит из двадцати аксиом: I1- I8, II1- II4, III1- III5, IV1, IV2, V*- Этот список отличается от списка аксиом Гильберта тем, что аксиома V заменена аксиомой V*. Эту систему аксиом коротко обозначим через
, что и в примере 2, которые обозначены соответственно словами «лежит на», «лежит между» и «равны». Список аксиом состоит из двадцати аксиом: I1- I8, II1- II4, III1- III5, IV1, IV2, V*- Этот список отличается от списка аксиом Гильберта тем, что аксиома V заменена аксиомой V*. Эту систему аксиом коротко обозначим через  A
A
Если база состоит из нескольких множеств, например из трех: Е, F, G, то иногда одно из этих множеств, например Е, играет основную роль в определяемых структурах. Тогда говорят, что эти структуры определены на множестве Е, а множества F и G рассматривают как вспомогательные.
4. Теория структур рода Т — это множество Г (Т) предложений (теорем), каждое из которых является логическим следствием аксиом системы  ,определяющих Т. Так, мы имеем теорию групп, теорию колец, теорию (геометрию) аффинных пространств, геометрию евклидовых пространств и т. д. Вместо Г(Т) иногда пишут: Г (
,определяющих Т. Так, мы имеем теорию групп, теорию колец, теорию (геометрию) аффинных пространств, геометрию евклидовых пространств и т. д. Вместо Г(Т) иногда пишут: Г ( ).
).
Математика занимается изучением математических структур. Основным ее методом служит аксиоматический метод: структура каждого рода определяется при помощи соответствующего списка аксиом, а дальше чисто логическим путем строится теория структур этого рода.
Таким образом, хотя математика в наше время и является чрезвычайно обширной отраслью знаний, имеющей многочисленные разделы и на первый взгляд разобщенные направления исследования, мы можем сказать, что математика — это единая наука. Ее предмет исследования — множество математических структур; ее основной метод — аксиоматический метод.
Дата публикования: 2015-11-01; Прочитано: 1068 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
