Аксиоматика А. В. Погорелова школьного курса геометрии

1. В современных учебных пособиях по геометрии для средней школы в основу построения курса положены системы аксиом, отличные от системы _H и от системы _W.

Рассмотрим сначала систему аксиом, предложенную в учебном пособии по геометрии для VI—Х классов средней школы А. В. Пого­релова 1. Для простоты изложения ограничимся рассмотрением системы аксиом планиметрии. Здесь база структуры евклидовой плоскости Е₂ состоит из трех множеств Е, F и R. Элементы из Е на­зываются точками, а элементы из F —прямыми; R - множество ве­щественных чисел. Множества Е и F выступают как основные, а множество R — как вспомогательное.

Основными отношениями являются следующие четыре отношения:

а) принадлежность точки и прямой; б) лежать между для трех точек одной прямой; в) длина отрезка; г) градусная мера угла.

1. Рассматриваемая система аксиом, которую мы обозначим через _р, состоит из девяти аксиом, разбитых на шесть групп.

I. Аксиомы принадлежности.

I₁. Каковы бы ни были две точки, существует прямая, проходящая

через эти точки, и притом только одна.

I₂. На каждой прямой лежат по крайней мере две точки. Существу­ют три точки, не лежащие на одной прямой.

II. Аксиомы порядка.

II₁. Из трех точек на прямой одна и только одна лежит между дву­мя другими.

На основе этой аксиомы вводится понятие отрезка. Отрезком АВ называется множество точек прямой, лежащих между точками А и В.

II₂. Прямая разбивает множество не принадлежащих ей точек плоскости на два подмножества (полуплоскости) так, что отрезок, соединяющий точки одной полуплоскости, не пересекается с прямой, а отрезок, соединяющий точки разных полуплоскостей, пересекается с прямой.

Затем вводятся понятия луча и треугольника. Лучом АВ с нача­лом А называется множество точек, состоящее из точки В и любой точки М прямой AB, такой, что точка А не лежит между точками В и М.

Треугольником называется фигура, состоящая из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков. Пользуясь аксиомой II₂, можно убедиться в том, что в теории Г ( _р) имеет место теорема, которая в аксиоматике Гильберта принимается за аксиому (аксиома Паша).

III. Аксиомы меры для отрезков и углов 1.

Обозначим через L, множество всех отрезков, а через R₊^* — мно­жество всех положительных чисел.

III₁. Если выбран некоторый отрезок EF, то существует отобра­жение l: L 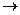R₊^*, такое, что выполняются два условия: а) если точ­ка С лежит между точками A и B, то l(АС) +l(СВ)=l(АВ); б) l(EF)=1.

Если l^/: L 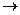R₊^* отображение при другом выборе отрезка E ^/F^/, то из равенства l(AB)=l(CD) следует: l ^/(AB)=l ^/(CD).

Число l(AB) называется длиной отрезка АВ, а отрезок EF— единичным отрезком.

Для того чтобы сформулировать следующую аксиому, введем понятие угла. Углом называется фигура, которая состоит из двух раз­личных лучей с общим началом. Угол называется развернутым, если эти лучи лежат на одной прямой. Мы будем говорить, что данный луч проходит между сторонами неразвернутого угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла. В случае развернутого угла мы считаем, что любой луч, исходящий из его вершины и отличный от его сторон, проходит между сторонами угла. Обозначим через множество всех углов.

III₂. Существует отображение : 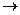R₊^*, такое, что выполняют­ся два условия:

а) если луч l проходит между сторонами угла hk, то (hl) + (lk) = (hk);

б) если hk — развернутый угол, то (hk) = 180.

Число (hk) называется градусной мерой угла hk.

Аксиома существования треугольника, рав­ного данному.

Два отрезка называются равными, если при любом выборе единичного отрезка их длины равны. Два угла называются равными, если они имеют одну и ту же градусную меру. Треугольники АВС и А ₁В ₁С ₁ называются равными, если выполняются равенства:

А = A₁, В= В₁, С= С₁, AB=A ₁B₁, BC=В₁ С ₁,AC=A ₁C ₁.

IV. Пусть АВС— треугольник и h —луч. Тогда существует треугольник A₁B₁C₁, равный треугольнику АВС, у которого верши­на А ₁ совпадает с началом луча h, вершина В ₁ лежит на луче h, а вер­шина C ₁ лежит в заданной полуплоскости относительно прямой, со­держащей луч h.

Пользуясь этой аксиомой, легко доказать следующие утвержде­ния:

1°. На данном луче от его начала можно отложить отрезок, рав­ный данному отрезку, и притом только один.

2°. От данного луча в заданную полуплоскость с границей, со­держащей данный луч, можно отложить угол, равный данному углу, и притом только один.

Аксиома существования отрезка данной длины.

V. Если выбран единичный отрезок, то, каково бы ни было вещест­венное число d > 0, существует отрезок длиной d.

Пользуясь аксиомой V и утверждениями 1° и 2°, можно доказать следующие два утверждения, которые из методических соображений в учебнике для средней школы приняты за аксиомы (аксиомы IV₁и IV₂).

3°. На данном луче от его начала можно отложить отрезок заданной длины и притом только один.

4°. От данного луча в данную полуплоскость с границей, содер­жащей данный луч, можно отложить угол с заданной градусной мерой, меньшей 180°, и притом только один.

Аксиома параллельных прямых.

Две прямые на плоскости называются параллельными, если они не пересекаются.

VI. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

1. Докажем теорему, аналогичную теореме 5 § 83.

Теорема. Система аксиом _р непротиворечива, если непротиво­речива арифметика вещественных чисел.

Доказательство:

Для доказательства теоремы достаточно убедиться в том, что все девять аксиом системы _р могут быть доказаны в теории Г ( _W) как теоремы (см. доказательство теоремы 5 § 83).

В § 16 и 17 мы убедились в том, что в теории Г ( _W) имеют место предложения I₁, I₂, II₁, II₂, III₁ и VI. Поэтому остается проверить выполнимость предложений III₂, IV и V.

III₂. Введем понятие градусной меры угла в теории Г ( _W). Пусть

(h, k) - произвольный угол, а и - векторы, принадлежащие соответственно направлениям лучей h и k. Радианной мерой угла hk назовем число , принадлежащее числово-му промежутку 0 < , такое, что

cos = ,

где g (, 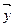)— билинейная форма, соответствующая выбранному единичному отрезку (см. ч. 1, § 18, п. 4). Нетрудно доказать, что cos не зависит от выбора единичного отрезка, а также от выбора век­торов и , принадлежащих направлениям лучей.

IV. Пусть АВС— треугольник, h— луч, исходящий из точки А₁, а — полуплоскость, границе которой принадлежит луч h. Рассмот­рим два флага (A, h₀, ₀) и (A ₁, h, ), где h ₀ — луч АВ, а ₀ — полуплос­кость с границей АВ, содержащая точку С. В §83 мы отметили, что теорема о задании движения с помощью двух флагов (ч. 1, §41, теоре­ма 2) имеет место в теории Г ( _W), поэтому существует движение f, которое переводит флаг (A, h₀, ₀) во флаг (A ₁, h, ). Если В₁ = f (В) и C₁ = f (С), то А ₁В₁ С ₁ искомый, так как В₁ h, С₁ и ABC = А ₁В₁ С ₁.

V. Пусть PQ — выбранный единичный отрезок, а d — любое положительное действительное число. Рассмотрим билинейную форму g(, 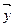), соответствующую отрезку PQ. Если А— произволь­ная точка плоскости, то существует точка В, такая, что = , где =d (аксиома 1 системы _W). Тогда