 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Взаимное расположение прямых на плоскости. Угол между двумя прямыми
|
|
Если две прямые l1 и l2 лежат на плоскости, то возможны три различных случая их взаимного расположения: 1)пересекаются (т.е. имеют одну общую точку); 2) параллельны и не совпадают; 3) совпадают.
Выясним, как узнать, какой из этих случаев имеет место, если эти прямые заданы своими уравнениями в общем виде:
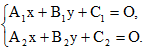 (12)
(12)
Если прямые l1 и l2 пересекаются в некоторой точке М(х,у), то координаты этой точки должны удовлетворять обоим уравнениям системы (12).
Следовательно, чтобы найти координаты точки пересечения прямых l1 и l2, надо решить систему уравнений (12):
1) если система (12) имеет единственное решение, то прямые l1 и l2 пересекаются;
2) если система (12) не имеет решения, то прямые l1 и l2 параллельны;
3) если система (12) имеет множество решений, то прямые l1 и l2 совпадают.
Условием совпадения двух прямых является пропорциональность соответствующих коэффициентов их уравнений.
Пример 10. Пересекаются ли прямые 3х+4у-1=0 и 2х+3у-1=0?
Решение: Решим систему уравнений: 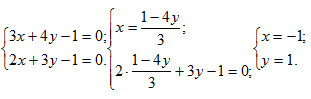 система имеет единственное решение, следовательно прямые пересекаются. Точка пересечения прямых имеет координаты (-1;1).
система имеет единственное решение, следовательно прямые пересекаются. Точка пересечения прямых имеет координаты (-1;1).
Пример 11. Параллельны, ли прямые 2х-у+2=0 и 4х-2у-1=0?
Решение: Решим систему уравнений 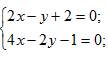
Эта система не имеет решений, следовательно прямые параллельны.
Пример 12. Совпадают ли прямые х+у+1=0 и 3х+3у+3=0?
Решение: Совпадают, так как коэффициенты пропорциональны.
Пример 13. Составить уравнение прямой линии, проходящей через точку пересечения прямых х+у-1=0, х-у+2=0 и через точку (2,1).
Решение: Находим координаты точки пересечения двух данных прямых линий. Для этого решаем данные уравнения совместно. Складывая, находим: 2х+1=0, откуда 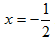
Вычитая из первого уравнения второе, получаем: 2у-3=0, откуда 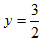 . Далее, остается составить уравнение прямой линии по двум точками (
. Далее, остается составить уравнение прямой линии по двум точками (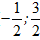 ) и (2;1)
) и (2;1)
Искомое уравнение будет 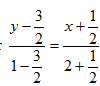 , или
, или 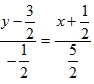 или
или 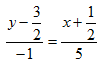 откуда
откуда 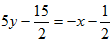 или x+5y-7=0
или x+5y-7=0
Углом между двумя прямыми на плоскости называется угол между их направляющими векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до 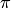 . В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина
. В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина 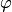 угла между двумя прямыми удовлетворяет условию
угла между двумя прямыми удовлетворяет условию 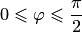 .
.
Если 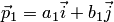 и
и 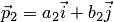 направляющие векторы прямых
направляющие векторы прямых 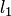 и
и 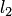 соответственно (рис.3.23,а), то величина
соответственно (рис.3.23,а), то величина 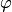 угла между этими прямыми вычисляется по формуле:
угла между этими прямыми вычисляется по формуле:
Чтобы получить величину 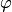 острого угла между прямыми, нужно правую часть взять по абсолютной величине:
острого угла между прямыми, нужно правую часть взять по абсолютной величине:
Угол 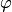 между прямыми (3.19) можно вычислить как угол между их нормалями
между прямыми (3.19) можно вычислить как угол между их нормалями 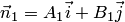 и
и 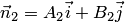 :
:
| (3.22) |
Чтобы получить величину 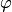 острого угла между прямыми, нужно правую часть взять по абсолютной величине:
острого угла между прямыми, нужно правую часть взять по абсолютной величине:
Необходимым и достаточным условием перпендикулярности прямых (3.19) является условие ортогональности их нормалей, т.е. равенства нулю скалярного произведения их нормалей 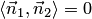 :
:
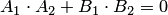
По формуле (3.22) получаем острый угол 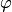 между прямыми (3.19), если
между прямыми (3.19), если 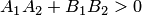 (рис.3.23,а), и тупой в противном случае:
(рис.3.23,а), и тупой в противном случае: 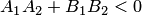 (рис.3.23,6). Другими словами, по формуле (3.22) находится тот угол между прямыми, в котором лежат точки, принадлежащие разноименным полуплоскостям, опреляемым данными прямыми. На рис.3.23 положительные и отрицательные полуплоскости отмечены знаками плюс "+" или минус "–" соответственно.
(рис.3.23,6). Другими словами, по формуле (3.22) находится тот угол между прямыми, в котором лежат точки, принадлежащие разноименным полуплоскостям, опреляемым данными прямыми. На рис.3.23 положительные и отрицательные полуплоскости отмечены знаками плюс "+" или минус "–" соответственно.
Если прямые заданы уравнениями с угловыми коэффициентами:
то угол 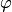 между ними (один из смежных углов) находится по формуле
между ними (один из смежных углов) находится по формуле
| (3.23) |
Если правая часть (3.23) положительна, то угол 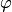 острый (рис.3.24), в противном случае — тупой. Чтобы получить острый угол
острый (рис.3.24), в противном случае — тупой. Чтобы получить острый угол 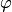 , нужно правую часть (3.23) взять по абсолютной величине:
, нужно правую часть (3.23) взять по абсолютной величине:
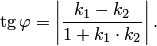
Если 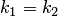 (условие параллельности прямых), то
(условие параллельности прямых), то 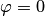 . Если
. Если 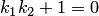 (условие перпендикулярности прямых), то правая часть (3.23) не определена
(условие перпендикулярности прямых), то правая часть (3.23) не определена 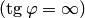 . Тогда полагают, что
. Тогда полагают, что 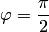 .
.
Дата публикования: 2015-10-09; Прочитано: 579 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
