Ортогон. м-цы и ортогон. преобразования

Квадратная невырожденная матрица называется ортогональной, если обратная к ней совпадает с транспонированной.

Теорема 1.15 Матрица ортогональна тогда и только тогда, когда она является матрицей перехода от одного ортонорма некоторого евклидова пространства к другому.

Доказательство. Пусть 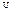- ортогональная матрица -ого порядка. Докажем, что ее столбцы образуют ортонормированный базис в .

Вычислим скалярное произведение -ого столбца на -ый: ,

так как транспонированный -ый столбец есть -ая строка транспонированной матрицы, совпадающей с обратной. Рассматривая столбцы матрицы 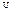как столбцы координат в каноническом базисе, получим, что матрица 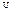есть матрица перехода от одного ортонорма (канонического базиса) в к другому (состоящему из столбцов данной матрицы).

Обратно, пусть и - два ортонорма в -мерном евклидовом пространстве, причем . Вычислим матрицу Грама для базиса : ,

так как матрица Грама любого ортонорма единичная. Отсюда, поскольку матрица 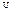, как матрица перехода, обратима, . Линейный оператор, действующий в конечномерном евклидовом пространстве, называется ортогональным, если он задается (в каком-то ортонорме) ортогональной матрицей. Таким образом, по определению, оператор ортогонален, если в некотором ортонорме он задан ортогональной матрицей:

,где .

§1. Множества точек в Rⁿ.

δ − окрестностью т. называется множество точек х, удовлетворяющих условию: , где δ − заданное положительное число. координатный прямоугольник со сторонами 2δ и центром в т. x^o.

Точка называется внутренней т. множества D, если Точка называется граничной т. множества D, если

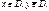Множество всех граничных точек называется границей множества D.

Множество, не содержащее ни одной граничной точки, называется открытым.

Множество, содержащее все свои граничные точки, называется замкнутым.

Множество называется связным, если две его любые точки можно соединить непрерывной кривой, целиком принадлежащей этому множеству. Областью называется связное открытое множество.

Множество называется односвязным, если любая непрерывная замкнутая кривая, принадлежащая множеству, может быть стянута в одну точку. В противном случае множество называется многосвязным (примеры).

Множество называется ограниченным, если оно целиком лежит внутри некоторой δ−окрестности и неограниченным в противном случае.

Любая ограниченная область, содержащая т. х^о называется окрестностью этой точки.

§2. Функции нескольких переменных. Основные определения и свойства.

Рассматривается множество . Если определено правило, по которому каждой точке ставится в соответствие некоторое число (единственным образом), то говорят, что на множестве D определена (однозначная) функция . Как обычно, множество D называется областью определения функции, а множество всех соответствующих значений u: Q = { u } – множеством значений. Часто функцию u = F (x) называют отображением области на мн-во UcR.

При n = 2 уравнение F (x,y) = C задает линии уровня поверхности z = F (x,y), а при n = 3 уравнение F (x,y,z) = С – поверхности уровня.

Задание ФНП может быть неявным: F (x,u) = 0 или параметрическим .

Теоремы об ограниченности непрерывной функции, о переходе через промежуточные значения и о достижении максимума и минимума формулируются для замкнутых областей. Верна также теорема о непрерывности сложной функции: пусть функция непрерывна в т. х^о, а функции в т. В этом случае функция

§3. Производные ФНП.

Рассмотрим функцию u = F (x), определенную в некоторой области D. Пусть − фиксированная точка. Дадим координате х ₁ приращение . Если существует конечный предел , то он называется частной производной функции F (x) по переменной х ₁ и обозначается

Аналогично определяются частные производные по всем остальным переменным.

§4. Частные производные высших порядков.

Вычисляя частные производные ФНП, мы снова получаем функцию тех же переменных, от которой можно взять частную производную, в том числе и по другой переменной (если она, конечно, существует): Частные производные по одной и той же переменной называются повторными, а по различным переменным – смешанными.

Теорема 1 (О равенстве смешанных производных). Пусть функция z = f (x, y) имеет вторые частные производные в окрестности т. М ₀, непрерывные в самой точке М ₀.

В этом случае

{Рассмотрим функции

Для 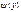аналогично получаем:

Из равенства следует

. Устремив h к нулю, в силу непрерывности производных, получаем: }

Если u = u (x ₁,…, x _n), то все вторые частные производные можно записать с помощью

.

Из т.1 следует, что матрица Гессе – симметрична.

§5. Дифференциал ФНП.

Пусть функция u = F (x) определена в области D и − фиксированная точка. Дадим приращение каждому аргументу x_i: Величину будем называть вектором приращения. В свою очередь функция u получит приращение равное

Определение 1. Функция u = F (x) называется дифференцируемой в т. х, если ее приращение может быть представлено в следующем виде: где A_i = A_i (x) и не зависит от Δ х, а − бесконечно малая при

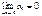
Величина вектора Δ х равна: Используя это обозначение, можно написать

Легко показать, что

{ }

Определение 2. Главная и линейная часть приращения дифференцируемой функции называется дифференциалом: Теорема 1. Функция, дифференцируемая в т. х ^o – непрерывна в этой точке. { }

Теорема 2. (Необходимое условие дифференцируемости) Если F (x) дифференцируема в т. х, то она имеет все частные производные в этой точке, причем

{Пусть }

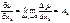Отсюда, 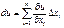Если х − независимая переменная, то и окончательно

Теорема 3. (Достаточное условие дифференцируемости) Пусть F (x) имеет все частные производные в окрестности т. х ^о, непрерывные в самой этой точке. Тогда функция дифференцируема в т. х ^о. {б/д}

Замечание. Для дифференцируемости функции одной переменной достаточно только существования производной.

Дифференциал функции u называют полным дифференциалом.

§6. Геометрический смысл дифференцируемости. Касательная плоскость и нормаль к поверхности.

Рассмотрим поверхность S: z = f (x,y), дифференцируемую в т. S.

Определение 1. Плоскость, проходящая через т. М ₀, называется касательной плоскостью к поверхности S в т. М ₀, если угол между ней и секущей (М ₀ М ₁) () стремится к нулю при .

Определение 2. Вектор, ортогональный к касательной плоскости в т. М ₀, называется нормальным вектором к поверхности в этой точке. Нормалью к поверхности называется

прямая, проходящая через т. М ₀ перпендикулярно касательной плоскости в этой точке.

Обозначим 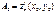, . Вектор приращения:

Из условия дифференцируемости функции z следует, что

Рассмотрим плоскость и угол φ между секущей и этой плоскостью: при 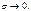Отсюда сразу следует, что плоскость П – касательная к поверхности в т. М ₀. В результате имеем:

Функция z = f (x,y), дифференцируемая в некоторой точке (х ₀, у ₀) имеет в соответствующей т. М ₀ касательную плоскость: и нормальный вектор

§7. Дифференциалы высших порядков.

Определение 1. Дифференциал от первого дифференциала функции называется вторым дифференциалом: Аналогично определяются дифференциалы более старших порядков.

Вычислим второй дифференциал функции двух переменных . При этом будем считать, что дифференциалы независимых переменных dx и dy – величины постоянные (т.е. не зависят от т.(х,у) и не меняются при вычислении каждого последующего дифференциала).

Не трудно видеть, что второй дифференциал представляет собой квадратичную форму от

переменных dx и dy. Матрица этой квадратичной формы есть матрица Гессе, т.е.

d ² z = (dx,dy)Г(dx,dy) ^T Кроме того,

второй дифференциал можно записать в символическом виде:

Дифференциал m – го порядка равен §9. Производная сложной функции.

Рассматривается сложная функция аргумента t:

Теорема 1. Пусть функции x _ţ дифференцируемы в т .t ^o, а функция u в соответствующей

т. х ^о. Тогда сложная функция u = u (t ₁,…, t _m) дифференцируема в т .t ^o, а ее частные производные в этой точке равны

{Доказательство проведем для частного случая (Изменятся только технические подробности) Пусть приращение t. Функции х и у получат приращения В свою очередь приращение u равно:

Так как o (Δ t) = o (Δ σ), окончательно получаем: }

§11. Неявные ФНП.

Рассмотрим уравнение F (u, x ₁,…, x _n) = 0. Будем считать, что по смыслу задачи u есть функция от переменных x_i: u = u (x ₁,…, x _n). В этом случае говорят, что u задана неявно.

Теорема 1 (О существовании и дифференцируемости неявной функции). Пусть функция u задана уравнением F (u, x) = 0 и функция F (u, x) удовлетворяет следующим условиям:

1) F (u, x) дифференцируема в окрестности т. М ₀(u ₀, x ⁰).

2) дифференцируема в окрестности т. М ₀ .

3) F (u ₀, x ⁰) = 0.

4)

Тогда для любого достаточно малого ε > 0 найдется δ > 0, такое, что в определена

единственная дифференцируемая функция u = f (x), удовлетворяющая условию

{без доказательства}

Для вычисления частных производных рассмотрим уравнение F (u, x, y) = 0. Пусть

u = u (x, y) – решение этого уравнения. Продифференцируем тождество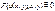

по х: Отсюда получаем (для у аналогично):

§12. Полная производная.

Пусть функции одной переменной. Тогда u есть функция одной переменной t и производная по единственному аргументу, т.е. –

обычная производная: §13. Производная по направлению. Градиент.

Рассматривается функция и единичный вектор . Проводится прямая l через т. М ₀ с направляющим вектором

Определение 1. Производная функции u = u (x, y, z) по переменной t называется производной по направлению l Так как на этой прямой u – сложная функция одной переменной, то производная по t равна полной произвдной по t

Она обозначается 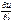и равна

Определение 2. Градиентом функции u (х ₁, х ₂,…, х _n) называется вектор, координаты которого равны частным производным функции u:

В нашем случае Таким образом, производная по направлению равна:

, где φ − угол между направляющим вектором прямой и градиентом функции в данной точке. Отсюда следует геометрический и физический смысл градиента функции (необходимо помнить, что скорость изменения функции вдоль прямой l):

1. Градиент ортогонален касательной плоскости к поверхности уровня в данной точке.

2. Градиент направлен в сторону максимального роста (изменения) функции в т. М ₀.

{Этот максимум достигается при φ = 0, т.е. при }

3. Величина наибольшей скорости роста функции равна .

§14. Локальный экстремум ФНП.

Рассматривается функция определенная на множестве .

Определение 1. Точка называется точкой локального экстремума, если: Из определения следует, что приращение функции 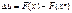не меняет знак в окрестности точки экстремума: если 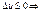в т. х ^о максимум, если минимум.

Теорема 1 (Необходимое условие локального экстремума). Пусть функция u = F (x) имеет в т. х ^о локальный экстремум. Если у нее в этой точке существуют частные производные, то они равны нулю.

{ Зафиксируем все переменные кроме х ₁ в т. х ^о: Тогда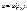

По Т. Ферма Для остальных переменных – аналогично }

Определение 2. Точка, в которой все частные производные равны нулю, называется стационарной.

Замечание 1. Функция, дифференцируемая в стационарной точке, имеет в ней дифференциал равный нулю: . Верно и обратное утверждение:

из равенства нулю дифференциала в некоторой точке следует стационарность этой точки.

Для доказательства достаточно взять все приращения аргументов кроме одного равными нулю. Тогда из формулы для дифференциала сразу следует равенство нулю соответствующей частной производной.

Замечание 2. Условия Т.1 не являются достаточными: u = xy, т. О(0,0).

Теорема 2 (Достаточное условие локального экстремума). Пусть функция u (x) дважды дифференцируема в стационарной точке. Если 2 – ой дифференциал в этой точке есть знакопостоянная квадратичная форма от дифференциалов независимых переменных, то функция в ней имеет экстремум: максимум, если и минимум, если

{Приращение функции в т. х^o по формуле Тейлора равно:

В достаточно малой окрестности знак приращения совпадает со знаком второго дифференциала функции u. В свою очередь, знакопостоянство квадратичной формы определяется его матрицей, т.е. матрицей Гессе (§4) и не меняется внутри окрестности стационарной точки в силу теоремы об устойчивости знака, что и доказывает теорему}

§15. Наибольшее и наименьшее значения функции в ограниченной замкнутой области.

Алгоритм поиска наибольшего и наименьшего значений функции в ограниченной замкнутой области сводится к решению трех задач:

1. Определение стационарных точек внутри области.

2. Определение стационарных точек на границе области.

3. Выбор наибольшего и наименьшего значений функции в этих точках.

Рассмотрим поставленную задачу на примере функции двух переменных. Требуется найти

наибольшее и наименьшее значения функции z = f (x, y), определенную замкнутой области

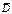с границей

1) Решаем систему

2)Решаем уравнение

3) Выбираем наибольшее и наименьшее значений функции в полученных точках.

§16. Условный экстремум ФНП.

Постановка задачи:

Найти экстремум функции при наличии дополнительных условий:

эти условия называют уравнениями связи

Определение 1. Точка х^о, удовлетворяющая уравнениям связи, называется точкой локального условного (относительного) экстремума, если такое, что для , являющегося решением уравнений связи, выполняется неравенство

Геометрическую интерпретацию легко видеть на примере функции двух переменных.

Пусть Целевая функция задает поверхность в пространстве, а уравнение связи − цилиндр с направляющей φ (х, у) = 0 и образующей параллельной оси ОZ.

Их пересечение – линия в пространстве, на которой нужно найти точки с локально экстремальными аппликатами.

Как и в случае обычного экстремума, необходимым условием является равенство нулю первого дифференциала функции и. Точки, удовлетворяющие этому условию и уравнениям связи, также будем называть стационарными.

Вообще говоря, из написанных условий следует, что m переменных являются функциями остальных n − m переменных. Если решить данную систему уравнений и подставить полученные решения в исходную функцию, то получится задача безусловного экстремума

для функции от n − m оставшихся переменных. При этом функцию u удобно записывать в виде ,где − решения уравнений связи (будем предполагать, что выполнены все условия теоремы существования и дифференцируемости системы функций, заданных неявно).

§17. Метод неопределенных множителей Лагранжа поиска условного экстремума.

Метод Лагранжа сводится к исследованию функции , называемой функцией Лагранжа и равной: (где λ_i − неизвестные постоянные параметры)