Преобразования базисов

Пусть задан в линейном пространстве L некоторый базис (e₁…e_n). Тогда любой вектор xЄL может быть разложен единственным образом по базису:

Док-во: Введем новый базис (e’₁…e’_n). В этом базисе тот же самый вектор x будет иметь уже другие координаты:

Введем в рассмотрение новый объект - векторную матрицу-строку. Это обычная матрица-строка, но ее элементами являются не числа, а векторы (из некоторого линейного пространства). Любую систему векторов можно задать в виде векторной матрицы строки. Для векторной матрицы-строки определим умножение ее справа на обычную числовую матрицу B размера mxp для данного m, равного числу векторов строки и произвольного p следующим образом:

С использованием векторных матриц-строк удобно записывать разложение произвольных систем векторов по данному базису.

Пусть дан базис (в виде векторной матрицы-строки) и система векторов . Запишем разложение векторов системы a по базису e:

Или, с использованием векторных матриц-строк:

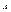, j-ый столбец матрицы - это столбец координат вектора в базисе .Если система линейно независима, то столбцы матрицы 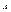линейно независимы.

Доказательство. Предположим противное - тогда найдутся числа , не все равные нулю, такие, что

,

или, покомпонентно:

С учетом этих равенств рассмотрим линейную комбинацию

Подставляя вместо каждого вектора 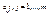, его разложение по базису , получим:

Итак, мы получили нетривиальную линейную комбинацию линейно независимых векторов, равную нулю, что невозможно.

Для одного вектора 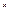его разложение по базису задается в виде:

, где 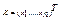- столбец координат вектора 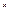в базисе .Вернемся к задаче преобразования базисов. Запишем разложение нового («штрихованного») базиса в старом (не «штрихованном»):

Матрица (квадратная порядка ) называется матрицей перехода от базиса к базису . Каждый ее столбец есть столбец координат соответствующего вектора нового базиса в старом базисе. Столбцы матрицы линейно независимы, тем самым ее ранг равен , и матрица является невырожденной. Тогда для разложения вектора 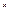в новом базисе получим:

Отсюда по теореме о единственности разложения вектора по базису

Так как матрица не вырождена, то

Если - матрица перехода от базиса к базису , то обратная матрица является матрицей перехода от базиса к базису .

Если - матрица перехода от базиса к базису , а - матрица перехода от базиса к базису , то - матрица перехода от базиса к базису .

Докво Пусть векторы базисов и заданы своими координатами в некотором базисе (который сам может быть явно и не определен). Требуется найти матрицу перехода от к . Составляем матрицы перехода от к и от к (по столбцам координат векторов базисов и ). Пусть это будут матрицы 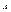и соответственно. Тогда используя утверждение получим