Сопряженный оператор

Пусть 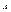- линейный оператор, являющийся преобразованием конечномерного евклидова пространства . Линейный оператор называется сопряженным к 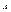, если для любых

Теорема 1.11 Для всякого линейного оператора - преобразования конечномерного евклидова пространства - существует единственный сопряженный.

Доказательство. Докажем сперва существование сопряженного оператора. Выберем в рассматриваемом пространстве произвольный ортонорм , и пусть . Возьмем транспонированную матрицу и определим оператор так, что для произвольного .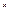

Тогда

Сопряженный оператор существует - он определяется матрицей, транспонированной к матрице исходного оператора.

Докажем теперь единственность сопряженного оператора. Пусть существует (вместе с ) такой линейный оператор , что .

Но тогда для любых векторов , откуда

Так как это равенство должно выполняться для любых , то ,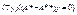

но это значит, что , или ,

и сопряженный оператор - единственный.